Story
PlanBot is a robot that has decided to accomplish the task of making a sandwich.

JuliaCon 2024
University of Maryland, College Park
Johns Hopkins University Applied Physics Laboratory
July 12, 2024
PlanBot is a robot that has decided to accomplish the task of making a sandwich.

PlanBot heads over to the kitchen.


*walk*
It seems like PlanBot’s is still processing (must still be waking up…).
50×50 Matrix{Int64}:
33 45 46 65 45 80 2 39 55 … 71 93 63 14 91 97 94 85
55 89 42 19 79 19 38 75 18 32 24 71 32 29 96 15 65
22 53 4 31 19 75 81 51 44 71 79 68 8 23 21 14 66
90 95 76 45 55 51 98 91 92 71 79 44 86 50 30 22 80
36 82 20 76 34 86 95 34 1 47 23 22 60 91 8 98 73
40 47 71 87 14 20 88 21 75 … 32 36 34 75 93 86 18 12
96 98 59 88 64 53 40 72 55 83 66 93 41 32 84 55 70
80 51 19 37 1 3 18 52 6 9 27 39 95 60 34 48 18
50 72 77 55 60 27 88 99 15 56 86 100 50 10 66 65 27
75 19 70 89 63 13 24 24 20 60 45 75 64 29 20 76 84
58 38 21 70 57 75 97 4 77 … 90 94 25 42 5 96 25 97
73 57 21 16 60 50 68 22 77 9 31 96 5 67 50 94 25
1 18 44 74 64 47 85 11 45 73 16 67 48 71 50 19 13
⋮ ⋮ ⋱ ⋮
71 90 6 77 31 19 23 57 95 97 75 3 42 33 99 23 41
10 36 64 82 36 6 16 74 35 37 56 50 24 14 78 96 37
85 73 41 96 68 6 96 95 28 … 39 49 91 44 97 18 76 87
35 41 43 52 49 99 29 19 53 15 85 23 26 46 94 97 44
77 32 32 65 3 88 48 5 60 73 54 88 28 68 34 36 38
27 81 89 46 88 57 39 40 80 16 12 81 5 32 97 100 42
54 11 84 94 11 53 60 64 74 66 32 98 89 100 7 52 50
30 50 91 68 18 21 79 15 11 … 7 39 44 19 24 88 21 84
25 56 7 52 83 56 88 48 26 37 14 87 47 58 84 53 37
98 49 63 51 52 73 37 28 7 79 47 63 50 22 32 67 77
86 50 95 8 86 13 68 1 66 95 54 30 78 36 19 27 86
71 94 48 89 39 9 34 20 89 79 79 68 38 12 100 74 34
Uhh…
Ah, that’s better!
(object LettuceSliced_1)
(receptacle LettuceSliced_1)
(lettuceslice LettuceSliced_1)
(clear LettuceSliced_1)
(ontable LettuceSliced_1)
(temperature LettuceSliced_1 RoomTemp)
(mass LettuceSliced_1 0.2)
(material LettuceSliced_1 Organic)
(object LettuceSliced_2)
(receptacle LettuceSliced_2)
(lettuceslice LettuceSliced_2)
(clear LettuceSliced_2)
(ontable LettuceSliced_2)
(temperature LettuceSliced_2 RoomTemp)
(mass LettuceSliced_2 0.2)
(material LettuceSliced_2 Organic)
(object LettuceSliced_3)
(receptacle LettuceSliced_3)
(lettuceslice LettuceSliced_3)
(clear LettuceSliced_3)
(ontable LettuceSliced_3)
(temperature LettuceSliced_3 RoomTemp)
(mass LettuceSliced_3 0.2)
(material LettuceSliced_3 Organic)
(object LettuceSliced_4)
(receptacle LettuceSliced_4)
(lettuceslice LettuceSliced_4)
(clear LettuceSliced_4)
(ontable LettuceSliced_4)
(temperature LettuceSliced_4 RoomTemp)
(mass LettuceSliced_4 0.2)
(material LettuceSliced_4 Organic)
(object LettuceSliced_5)
(receptacle LettuceSliced_5)
(lettuceslice LettuceSliced_5)
(clear LettuceSliced_5)
(ontable LettuceSliced_5)
(temperature LettuceSliced_5 RoomTemp)
(mass LettuceSliced_5 0.2)
(material LettuceSliced_5 Organic)
(object TomatoSliced_1)
(receptacle TomatoSliced_1)
(tomatoslice TomatoSliced_1)
(clear TomatoSliced_1)
(ontable TomatoSliced_1)
(temperature TomatoSliced_1 RoomTemp)
(mass TomatoSliced_1 0.3)
(material TomatoSliced_1 Organic)
(object TomatoSliced_2)
(receptacle TomatoSliced_2)
(clear TomatoSliced_2)
(tomatoslice TomatoSliced_2)
(ontable TomatoSliced_2)
(temperature TomatoSliced_2 RoomTemp)
(mass TomatoSliced_2 0.3)
(material TomatoSliced_2 Organic)
(object TomatoSliced_3)
(receptacle TomatoSliced_3)
(tomatoslice TomatoSliced_3)
(clear TomatoSliced_3)
(ontable TomatoSliced_3)
(temperature TomatoSliced_3 RoomTemp)
(mass TomatoSliced_3 0.3)
(material TomatoSliced_3 Organic)
(object TomatoSliced_4)
(receptacle TomatoSliced_4)
(tomatoslice TomatoSliced_4)
(clear TomatoSliced_4)
(ontable TomatoSliced_4)
(temperature TomatoSliced_4 RoomTemp)
(mass TomatoSliced_4 0.3)
(material TomatoSliced_4 Organic)
(object TomatoSliced_5)
(receptacle TomatoSliced_5)
(tomatoslice TomatoSliced_5)
(clear TomatoSliced_5)
(ontable TomatoSliced_5)
(temperature TomatoSliced_5 RoomTemp)
(mass TomatoSliced_5 0.3)
(material TomatoSliced_5 Organic)
(object TomatoSliced_6)
(receptacle TomatoSliced_6)
(tomatoslice TomatoSliced_6)
(clear TomatoSliced_6)
(ontable TomatoSliced_6)
(temperature TomatoSliced_6 RoomTemp)
(mass TomatoSliced_6 0.3)
(material TomatoSliced_6 Organic)
(object TomatoSliced_7)
(receptacle TomatoSliced_7)
(tomatoslice TomatoSliced_7)
(clear TomatoSliced_7)
(ontable TomatoSliced_7)
(temperature TomatoSliced_7 RoomTemp)
(mass TomatoSliced_7 0.3)
(material TomatoSliced_7 Organic)
(object TomatoSliced_8)
(receptacle TomatoSliced_8)
(tomatoslice TomatoSliced_8)
(clear TomatoSliced_8)
(ontable TomatoSliced_8)
(temperature TomatoSliced_8 RoomTemp)
(mass TomatoSliced_8 0.3)
(material TomatoSliced_8 Organic)
(object TomatoSliced_9)
(receptacle TomatoSliced_9)
(tomatoslice TomatoSliced_9)
(clear TomatoSliced_9)
(ontable TomatoSliced_9)
(temperature TomatoSliced_9 RoomTemp)
(mass TomatoSliced_9 0.3)
(material TomatoSliced_9 Organic)
(object TomatoSliced_10)
(receptacle TomatoSliced_10)
(tomatoslice TomatoSliced_10)
(clear TomatoSliced_10)
(ontable TomatoSliced_10)
(temperature TomatoSliced_10 RoomTemp)
(mass TomatoSliced_10 0.3)
(material TomatoSliced_10 Organic)
(object Plate_1)
(receptacle Plate_1)
(plate Plate_1)
(clear Plate_1)
(ontable Plate_1)
(temperature Plate_1 RoomTemp)
(mass Plate_1 0.4)
(material Plate_1 Ceramic)
(object Plate_2)
(receptacle Plate_2)
(plate Plate_2)
(clear Plate_2)
(ontable Plate_2)
(temperature Plate_2 RoomTemp)
(mass Plate_2 0.4)
(material Plate_2 Ceramic)
(object Plate_3)
(receptacle Plate_3)
(plate Plate_3)
(clear Plate_3)
(ontable Plate_3)
(temperature Plate_3 RoomTemp)
(mass Plate_3 0.4)
(material Plate_3 Ceramic)
(object Knife_1)
(knife Knife_1)
(clear Knife_1)
(ontable Knife_1)
(temperature Knife_1 RoomTemp)
(mass Knife_1 0.5)
(material Knife_1 Metal)
(object BreadSliced_1)
(receptacle BreadSliced_1)
(breadslice BreadSliced_1)
(clear BreadSliced_1)
(ontable BreadSliced_1)
(temperature BreadSliced_1 RoomTemp)
(mass BreadSliced_1 0.1)
(material BreadSliced_1 Organic)
(object BreadSliced_2)
(receptacle BreadSliced_2)
(breadslice BreadSliced_2)
(clear BreadSliced_2)
(ontable BreadSliced_2)
(temperature BreadSliced_2 RoomTemp)
(mass BreadSliced_2 0.1)
(material BreadSliced_2 Organic)
(object BreadSliced_3)
(receptacle BreadSliced_3)
(breadslice BreadSliced_3)
(clear BreadSliced_3)
(ontable BreadSliced_3)
(temperature BreadSliced_3 RoomTemp)
(mass BreadSliced_3 0.1)
(material BreadSliced_3 Organic)
(object BreadSliced_4)
(receptacle BreadSliced_4)
(breadslice BreadSliced_4)
(clear BreadSliced_4)
(ontable BreadSliced_4)
(temperature BreadSliced_4 RoomTemp)
(mass BreadSliced_4 0.1)
(material BreadSliced_4 Organic)
(object BreadSliced_5)
(receptacle BreadSliced_5)
(breadslice BreadSliced_5)
(clear BreadSliced_5)
(ontable BreadSliced_5)
(temperature BreadSliced_5 RoomTemp)
(mass BreadSliced_5 0.1)
(material BreadSliced_5 Organic)
Now, what’s the plan?

Goal
# tomato-on-lettuce sandwich on a plate
(object A) (object B) (object C) (object D)
(object E) (tomatoslice A) (lettucesliced B)
(breadsliced C) (breadsliced D) (plate E)
(on C E) (on B C) (on A B) (on D A)Based on PDDL (Knoblock et al. 1998)
Predicates
(object ?x)
(receptacle ?x)
(lettuceslice ?x)
(tomatoslice ?x)
(breadloaf ?x)
(breadslice ?x)
(plate ?x)
(knife ?x)
(temperature ?x ?y)
(mass ?x ?y)
(material ?x ?y)
(ispartof ?x ?y)
(holding ?x)
(arm-empty)
(clear ?x)
(ontable ?x)
(on ?x ?y)Stack Action
(:action stack
:parameters (?ob ?underob)
:precondition (and (clear ?underob) (holding ?ob))
:effect (and (arm-empty) (clear ?ob) (on ?ob ?underob)
(not (clear ?underob)) (not (holding ?ob))))World State
(object LettuceSliced_1)
(receptacle LettuceSliced_1)
(lettuceslice LettuceSliced_1)
(clear LettuceSliced_1)
(ontable LettuceSliced_1)
(holding BreadSliced_1)
(object BreadSliced_1)
(receptacle BreadSliced_1)
(breadslice BreadSliced_1)
(clear BreadSliced_1)
(ontable BreadSliced_1)
(temperature BreadSliced_1 RoomTemp)
(mass BreadSliced_1 0.1)
(material BreadSliced_1 Organic)
Goal
# tomato-on-lettuce sandwich on a plate
(object A) (object B) (object C) (object D)
(object E) (tomatoslice A) (lettucesliced B)
(breadsliced C) (breadsliced D) (plate E)
(on C E) (on B C) (on A B) (on D A)Based on PDDL (Knoblock et al. 1998)
Predicates
(object ?x)
(receptacle ?x)
(lettuceslice ?x)
(tomatoslice ?x)
(breadloaf ?x)
(breadslice ?x)
(plate ?x)
(knife ?x)
(temperature ?x ?y)
(mass ?x ?y)
(material ?x ?y)
(ispartof ?x ?y)
(holding ?x)
(arm-empty)
(clear ?x)
(ontable ?x)
(on ?x ?y)Stack Action
(:action stack
:parameters (?ob ?underob)
:precondition (and (clear ?underob) (holding ?ob))
:effect (and (arm-empty) (clear ?ob) (on ?ob ?underob)
(not (clear ?underob)) (not (holding ?ob))))World State
(object LettuceSliced_1)
(receptacle LettuceSliced_1)
(lettuceslice LettuceSliced_1)
(clear LettuceSliced_1)
(ontable LettuceSliced_1)
(arm-empty)
(on BreadSliced_1 LettuceSliced_1)
(object BreadSliced_1)
(receptacle BreadSliced_1)
(breadslice BreadSliced_1)
(clear BreadSliced_1)
(ontable BreadSliced_1)
(temperature BreadSliced_1 RoomTemp)
(mass BreadSliced_1 0.1)
(material BreadSliced_1 Organic)
Goal
# tomato-on-lettuce sandwich on a plate
(object A) (object B) (object C) (object D)
(object E) (tomatoslice A) (lettucesliced B)
(breadsliced C) (breadsliced D) (plate E)
(on C E) (on B C) (on A B) (on D A)Based on PDDL (Knoblock et al. 1998)
Predicates
(object ?x)
(receptacle ?x)
(lettuceslice ?x)
(tomatoslice ?x)
(breadloaf ?x)
(breadslice ?x)
(plate ?x)
(knife ?x)
(temperature ?x ?y)
(mass ?x ?y)
(material ?x ?y)
(ispartof ?x ?y)
(holding ?x)
(arm-empty)
(clear ?x)
(ontable ?x)
(on ?x ?y)Stack Action
(:action stack
:parameters (?ob ?underob)
:precondition (and (clear ?underob) (holding ?ob))
:effect (and (arm-empty) (clear ?ob) (on ?ob ?underob)
(not (clear ?underob)) (not (holding ?ob))))World State
(object LettuceSliced_1)
(receptacle LettuceSliced_1)
(lettuceslice LettuceSliced_1)
(clear LettuceSliced_1)
(ontable LettuceSliced_1)
(arm-empty)
(on BreadSliced_1 LettuceSliced_1)
(object BreadSliced_1)
(receptacle BreadSliced_1)
(breadslice BreadSliced_1)
(tomatoslice BreadSliced_1)
(clear BreadSliced_1)
(ontable BreadSliced_1)
(temperature BreadSliced_1 RoomTemp)
(mass BreadSliced_1 0.1)
(material BreadSliced_1 Organic)\[ \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\cat}[1]{\mathsf{#1}} \newcommand{\CAT}[1]{\mathsf{#1}} \newcommand{\Set}{\CAT{Set}} \DeclareMathOperator{\Path}{Path} \newcommand{\catSet}[1]{\cat{#1}\text{-}\Set} \DeclareMathOperator{\Ob}{Ob} \DeclareMathOperator{\Hom}{Hom} \]
Wants to be able to model everything about the world.
But having many predicates can result in expressive states which can cause a combinatorial explosion of the search space.
Wants the world state to be valid according to an implicit model.
But this representation does not allow you to express complex knowledge constraints.
Wants actions to be defined generically.
But this representation requires that all action preconditions and effects are explicit in the action model.

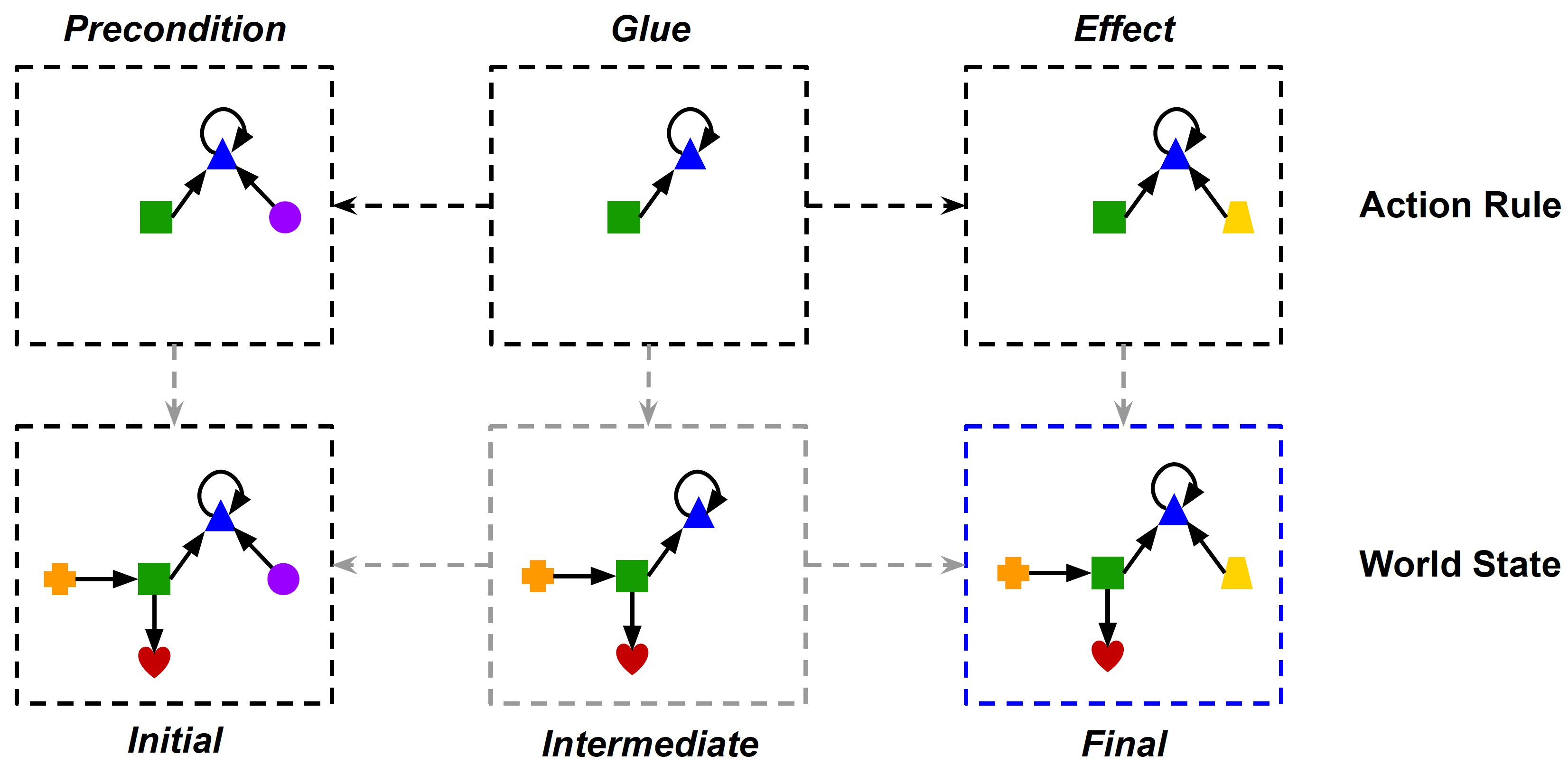
Action rules and pushouts are in \(\catSet{C}\).
Definition: A \(\cat{C}\)-set is a functor from \(\cat{C} \rightarrow \cat{Set}\). \(\cat{C}\) is referred to as the schema category. \(\cat{Set}\) is a category whose objects are sets and whose morphisms are set function maps.
Example: An example \(\cat{C}\)-set, called \(X\), that stores data about people’s favorite pet.
The category of elements construction (Riehl 2016) enables interoperability of \(X\) with RDF syntax for knowledge graphs (Spivak and Kent 2012).
Definition: A functor, \(F: \cat{C} \rightarrow \cat{D}\), from a category \(\cat{C}\) to a category \(\cat{D}\), has two components, \(F_0\) and \(F_1\), where:
\(F_0\) is a map between objects
\(F_0: \text{Ob}(\cat{C}) \rightarrow \text{Ob}(\cat{D})\)
\(F_1\) is a map between morphism sets
\(F_1: \text{Hom}_\cat{C}(X, Y) \rightarrow \text{Hom}_\cat{D}(F_0(X), F_0(Y))\)
such that,
Definition: For functors, \(F: \cat{C} \rightarrow \cat{D}\) and \(G: \cat{C} \rightarrow \cat{D}\), a natural transformation between \(\alpha: F \rightarrow G\) that associates every object in \(C\) and with a morphism in \(D\) such that composition is preserved.
Definition: The category \(\catSet{C}\) is a category whose objects are \(\cat{C}\)-set functors and whose morphisms are natural transformations.
A span in \(\catSet{C}\) is a diagram of shape (\(\bullet \leftarrow \bullet \rightarrow \bullet\)) in \(\catSet{C}\).
In this approach, spans are presented as colimits of representable functors. This means connected objects (via outgoing morphisms) in \(\cat{C}\) are also matched during rewriting.
using Catlab
using AlgebraicRewriting
@present OntBreadOnly(FreeSchema) begin
## Objects
Thing::Ob
BreadLoaf::Ob
BreadSlice::Ob
Countertop::Ob
Stool::Ob
## Morphisms
f::Hom(BreadSlice, BreadLoaf) # is part of
g::Hom(BreadLoaf, Thing) # is-a
h::Hom(Countertop, Thing) # is-a
l::Hom(Stool, Thing) # is-a
## Relations
InOn::Ob
inOn_l::Hom(InOn, Thing)
inOn_r::Hom(InOn, Thing)
end
# Create a C-set type based on ontology
const BreadOnly = DynamicACSet("BreadOnly", OntBreadOnly)
OntBreadOnly schema
state = @acset_colim yBreadOnly begin
# Items in the scene
myCountertop::Countertop
myStool::Stool
naturesOwn::BreadLoaf
(slice0, slice1, slice2)::BreadSlice
# Nature's Own Breadloaf has three slices
# f::Hom(BreadSlice, BreadLoaf)
f(slice0) == naturesOwn # is part of
f(slice1) == naturesOwn # is part of
f(slice2) == naturesOwn # is part of
# Breadloaf is on countertop (relation)
thing_on_thing::InOn
inOn_l(thing_on_thing) == naturesOwn
inOn_r(thing_on_thing) == myCountertop
# Breadloaf, counterop, and stool are things
# g::Hom(BreadLoaf, Thing)
# h::Hom(Countertop, Thing)
# l::Hom(Stool, Thing)
(thing1, thing2, thing3)::Thing
g(naturesOwn) == thing1
h(myCountertop) == thing2
l(myStool) == thing3
end
pretty_tables(state)┌───────────┬───┐
│ BreadLoaf │ g │
├───────────┼───┤
│ 1 │ 2 │
└───────────┴───┘
┌────────────┬───┐
│ BreadSlice │ f │
├────────────┼───┤
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 1 │
└────────────┴───┘
┌────────────┬───┐
│ Countertop │ h │
├────────────┼───┤
│ 1 │ 1 │
└────────────┴───┘
┌───────┬───┐
│ Stool │ l │
├───────┼───┤
│ 1 │ 3 │
└───────┴───┘
┌──────┬────────┬────────┐
│ InOn │ inOn_l │ inOn_r │
├──────┼────────┼────────┤
│ 1 │ 2 │ 1 │
└──────┴────────┴────────┘
d = DRule(@migration(SchRule, OntBreadOnly, begin
L => @join begin
(thing1, thing2)::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
g(breadloaf) == thing1
h(countertop) == thing2
thing_on_thing::InOn
inOn_l(thing_on_thing) == breadloaf
inOn_r(thing_on_thing) == countertop
end
K => @join begin
thing::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
end
R => @join begin
(thing1, thing2)::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
g(breadloaf) == thing1
h(stool) == thing2
thing_on_thing::InOn
inOn_l(thing_on_thing) == breadloaf
inOn_r(thing_on_thing) == stool
end
l => begin
thing => thing1
breadloaf => breadloaf
countertop => countertop
stool => stool
end
r => begin
thing => thing1
breadloaf => breadloaf
countertop => countertop
stool => stool
end
end))
new_state = apply_rule(move_bread_action, state)
pretty_tables(new_state)
#=
Thing::Ob
BreadLoaf::Ob
BreadSlice::Ob
Countertop::Ob
Stool::Ob
f::Hom(BreadSlice, BreadLoaf) # is part of
g::Hom(BreadLoaf, Thing) # is-a
h::Hom(Countertop, Thing) # is-a
l::Hom(Stool, Thing) # is-a
InOn::Ob
inOn_l::Hom(InOn, Thing)
inOn_r::Hom(InOn, Thing)
=#┌───────────┬───┐
│ BreadLoaf │ g │
├───────────┼───┤
│ 1 │ 1 │
└───────────┴───┘
┌────────────┬───┐
│ BreadSlice │ f │
├────────────┼───┤
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 1 │
└────────────┴───┘
┌────────────┬───┐
│ Countertop │ h │
├────────────┼───┤
│ 1 │ 3 │
└────────────┴───┘
┌───────┬───┐
│ Stool │ l │
├───────┼───┤
│ 1 │ 2 │
└───────┴───┘
┌──────┬────────┬────────┐
│ InOn │ inOn_l │ inOn_r │
├──────┼────────┼────────┤
│ 1 │ 1 │ 2 │
└──────┴────────┴────────┘
flowchart BT
A("`**ACSets.jl**
ACSets: Algebraic databases
as in-memory data structures`") --> B("`**Catlab.jl**
A framework for applied
category theory in the
Julia language`")
%% E("`**CompTime.jl**
%% Library for compile-time
%% computing in Julia`") --> C("`**AlgebraicRewriting.jl**
%% Implementations of algebraic
%% rewriting techniques like
%% DPO, SPO, SqPO`")
B("`**Catlab.jl**
A framework for applied
category theory in the
Julia language`") --> C("`**AlgebraicRewriting.jl**
Implementations of algebraic
rewriting techniques like
DPO, SPO, SqPO`")
A("`**ACSets.jl**
ACSets: Algebraic databases
as in-memory data structures`") --> C("`**AlgebraicRewriting.jl**
Implementations of algebraic
rewriting techniques like
DPO, SPO, SqPO`")
%% B("`**Catlab.jl**
%% A framework for applied
%% category theory in the
%% Julia language`") --> G("`**AlgebraicPetri.jl**
%% Build Petri net models
%% compositionally`")
B("`**Catlab.jl**
A framework for applied
category theory in the
Julia language`") --> D("`**DataMigrations.jl**
Package for contravariant
data migrations using
Catlab`")
A("`**ACSets.jl**
ACSets: Algebraic databases
as in-memory data structures`") --> D("`**DataMigrations.jl**
Package for contravariant
data migrations using
Catlab`")
%% F("`**GATlab.jl**
%% GATlab: a computer algebra
%% system based on generalized
%% algebraic theories (GATs)`") --> D("`**DataMigrations.jl**
%% Package for contravariant
%% data migrations using
%% Catlab`")
%% E("`**CompTime.jl**
%% Library for compile-time
%% computing in Julia`") --> D("`**DataMigrations.jl**
%% Package for contravariant
%% data migrations using
%% Catlab`")
%% F("`**GATlab.jl**
%% GATlab: a computer algebra
%% system based on generalized
%% algebraic theories (GATs)`") --> B("`**Catlab.jl**
%% A framework for applied
%% category theory in the
%% Julia language`")
%% E("`**CompTime.jl**
%% Library for compile-time
%% computing in Julia`") --> B("`**Catlab.jl**
%% A framework for applied
%% category theory in the
%% Julia language`")
%% linkStyle 1,2,3,4,5 stroke:#333,stroke-width:3px
style A fill:#e4f1f5,stroke:#333,stroke-width:2px
style B fill:#e4f1f5,stroke:#333,stroke-width:2px
style C fill:#e4f1f5,stroke:#333,stroke-width:2px
style D fill:#e4f1f5,stroke:#333,stroke-width:2px
click A "https://github.com/AlgebraicJulia/ACSets.jl"
click B "https://github.com/AlgebraicJulia/Catlab.jl"
click C "https://github.com/AlgebraicJulia/AlgebraicRewriting.jl"
click D "https://github.com/AlgebraicJulia/DataMigrations.jl"
@acset_colim for defining world states using diagrammatic syntax.data = @acset_colim yTowersOfHanoi begin
(disk1, disk2, disk3)::Disk
(peg1, peg2)::Peg
(smaller1, smaller2, smaller3)::Smaller
isSmaller_l(smaller1) == disk1 # disk1 < disk2
isSmaller_r(smaller1) == disk2
isSmaller_l(smaller2) == disk2 # disk2 < disk3
isSmaller_r(smaller2) == disk3
isSmaller_l(smaller3) == disk1 # disk1 < disk3
isSmaller_r(smaller3) == disk3
diskIsOnPeg(disk1) == peg1
diskIsOnPeg(disk2) == peg1
diskIsOnPeg(disk3) == peg2
isClear(disk1) == true
isClear(disk2) == false
isClear(disk3) == true
endACSetInterface.codom_parts(acs::StructACSet{S}, f::Symbol) where {S} = _codom_parts(acs, Val{S}, Val{f})
ACSetInterface.codom_parts(acs::DynamicACSet, f::Symbol) = runtime(_codom_parts, acs, acs.schema, f)

Using our approach, we can:
 Evan Patterson
Evan Patterson
 Kris Brown
Kris Brown
 Kevin Arlin
Kevin Arlin
 Owen Lynch
Owen Lynch
Research Software Engineers

 Angeline Aguinaldo
Angeline Aguinaldo
Ph.D. Candidate
University of Maryland, College Park
 James Fairbanks
James Fairbanks
Assistant Professor
University of Florida
 Jaime Ruiz
Jaime Ruiz
Associate Professor
University of Florida
 William Regli
William Regli
Professor
University of Maryland, College Park

Angeline Aguinaldo
University of Maryland, College Park
Johns Hopkins University Applied Physics Laboratory
email: [email protected]
website: angelineaguinaldo.com
Definition: A category, \(\cat{C}\), consists of:
satisfying the associativity law \(h \circ (g \circ f) = (h \circ g) \circ f\) and unitality laws \(f \circ 1_x = f\) and \(1_y \circ f = f\) whenever these equations make sense.
Use functorial data migration (Spivak 2012) to translate actions to new domain ontologies
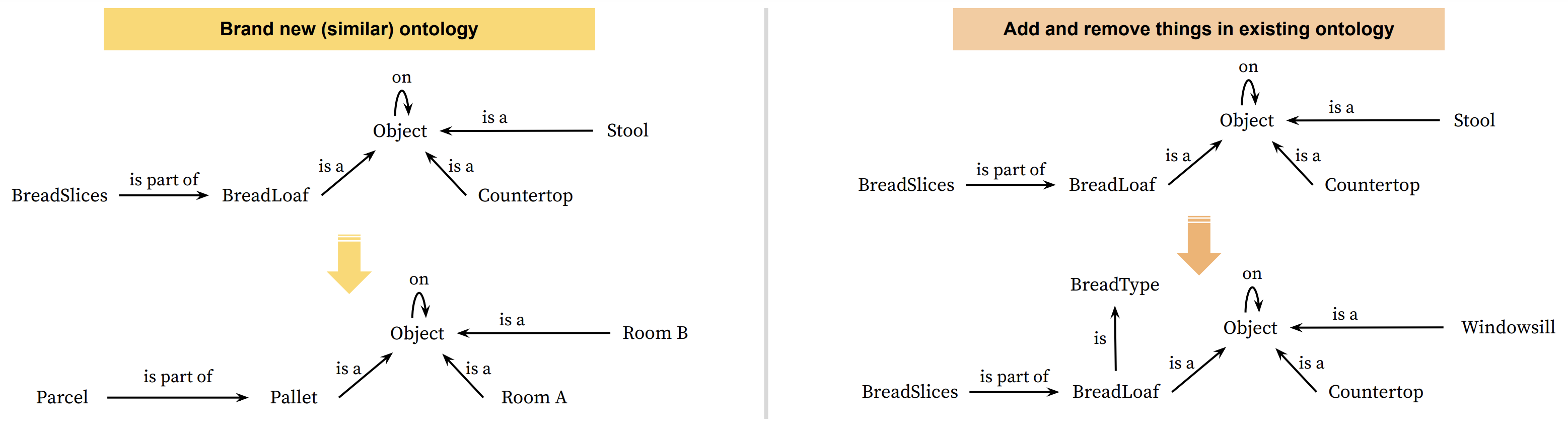
Leverage composition to factor out preconditions to support hierarchical planning.
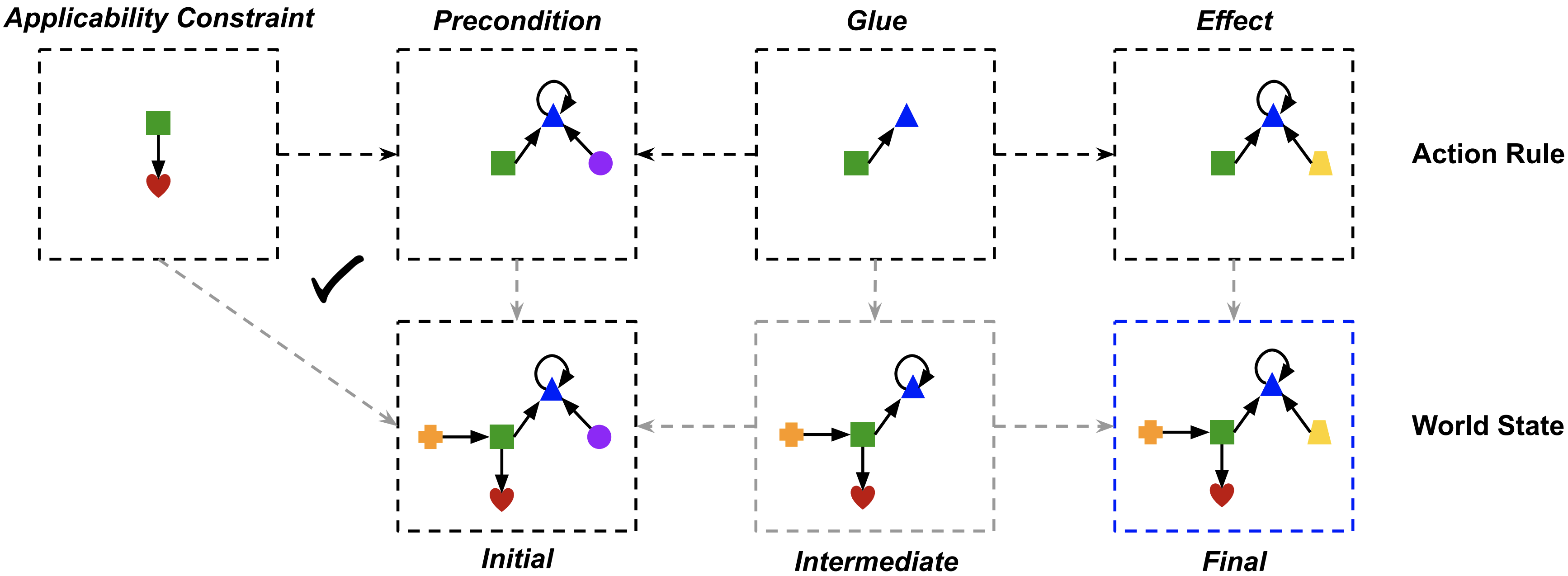

JuliaCon 2024