Analogical Plan Transfer in Robotics using Functorial Data Migrations
Applied Category Theory Special Session
AMS Joint Mathematics Meeting 2025
January 8, 2025
Plan Transfer in Robotics
Transfer plan from the source (left) to the target (right) planning domain
Humanoid robot
Arms
Bins
Mobile robot
Lift
Box
Problem: Designing planning problems and running planners is time-consuming.
(Alnazer and Georgievski 2023) (Ingrand and Ghallab 2017)
\[ \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\cat}[1]{\mathsf{#1}} \newcommand{\CAT}[1]{\mathsf{#1}} \newcommand{\Set}{\CAT{Set}} \DeclareMathOperator{\Path}{Path} \newcommand{\catSet}[1]{\cat{#1}\text{-}\Set} \DeclareMathOperator{\Ob}{Ob} \DeclareMathOperator{\Hom}{Hom} \]
Analogies from Cognitive Psychology
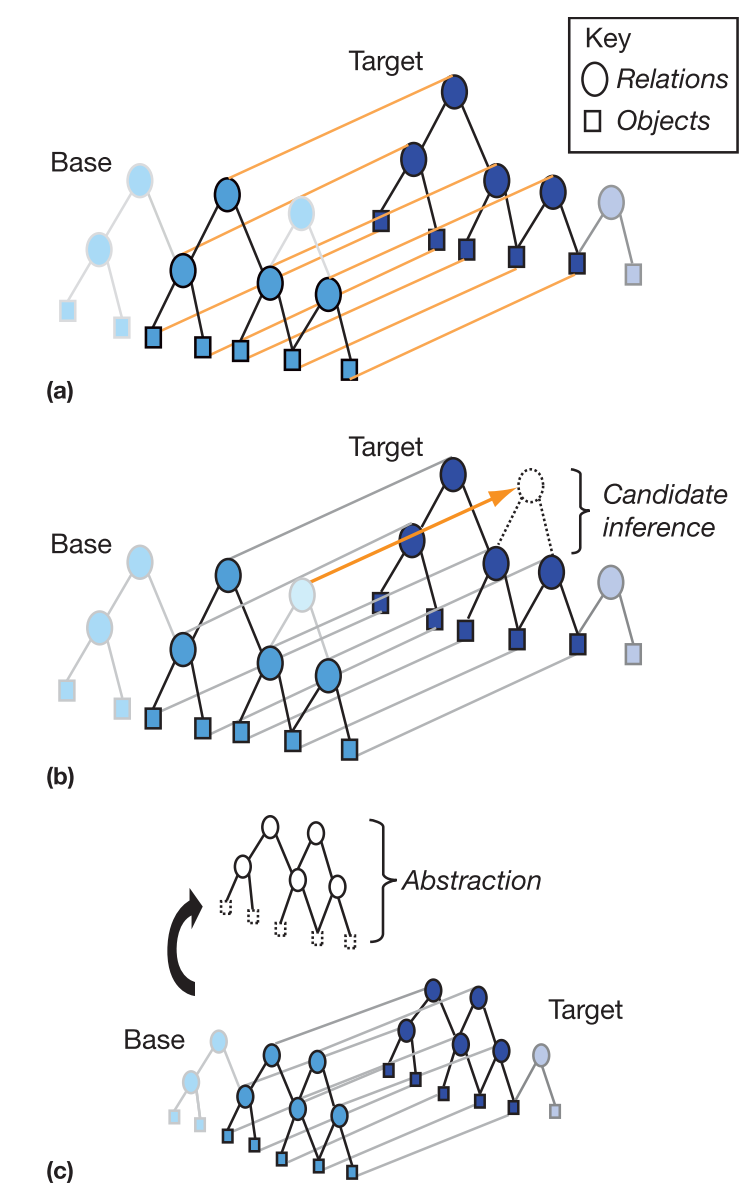
(Gentner and Smith 2012)
Informal Definition: (Analogical Plan Transfer) Analogical plan transfer identifies structural similarities, or analogies, between planning domains and leverages these analogies to adapt plans from one domain to another. (Aguinaldo 2024)
Why analogies?
(Wilkins and DesJardins 2001) argued that an ideal planning system should mimic human behavior by using analogies to transfer solutions from one problem to another.
What are analogies?
According to (Gentner 1983), analogies:
- have a one-to-one correspondence, each concept in the source domain maps to at most one concept in the target domain
- adhere to the systematicity principle, where analogical maps connect large, densely connected systems of concepts, instead of just a handful of isolated concepts
Types of Analogies (in analogical plan transfer)
Analogies with Task Planning
PDDL1 does not have built-in support for domain comparison or domain ontology alignment. Therefore, a new planning language that supports these capabilities is a prerequisite for analogical plan transfer. (Aguinaldo 2024)
State Transition System Model for Planning
- States, \(S = \{s_0, s_1, s_2, \dots\}\) set of all possible states
- Actions, \(A = \{a_0, a_1, a_2, \dots\}\) set of all possible actions
- Preconditions, \(\mathrm{Pre}(a)\) conditions that must be true in the state for the action to be applied
- Effects, \(\mathrm{Eff}(a)\) conditions are true in the state after the action is applied
- Transition function, \(\gamma: A \times S \rightarrow S\) partial function that maps an action and a state to the resulting state
- Checking applicability an action \(a \in A\) is at state \(s \in S\) if \(\gamma(a, s)\) is defined
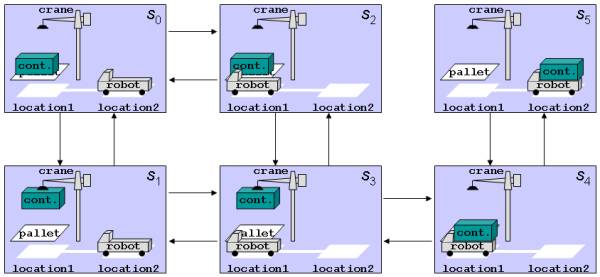
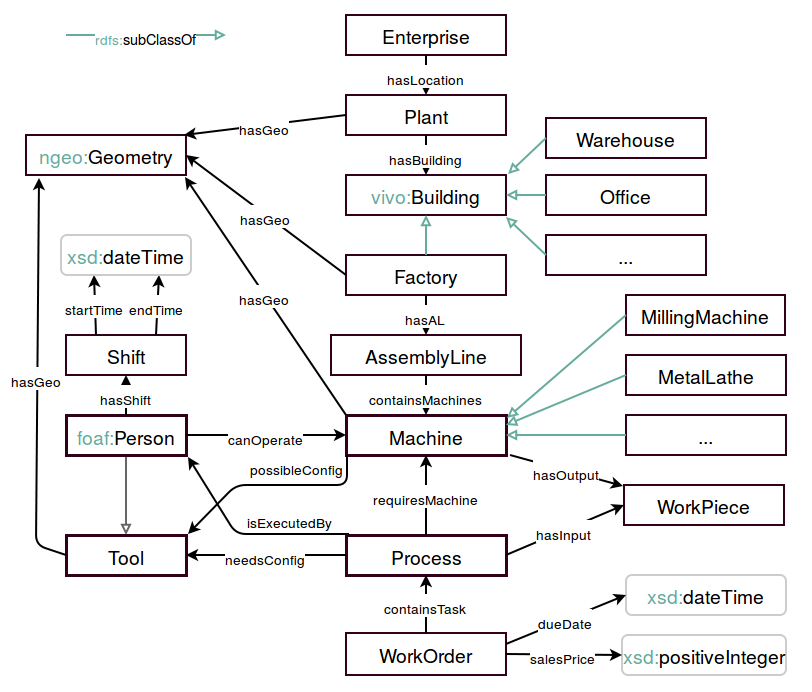
Planning States as \(\cat{C}\)-sets
Definition: (\(\cat{C}\)-set, schema category) A \(\cat{C}\)-set is a functor from \(\cat{C} \rightarrow \cat{Set}\). \(\cat{C}\) is referred to as the schema category (i.e. ontology). \(\cat{Set}\) is a category whose objects are sets and whose morphisms are set function maps.
Example:
A \(\cat{C}\)-set, \(X\), that stores data about what boxes are on which surface.
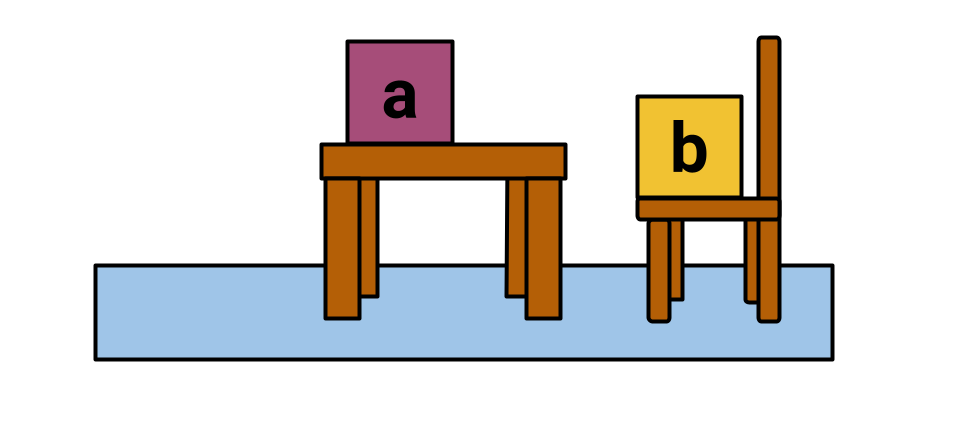
The category of elements construction (Riehl 2016) makes \(X\) interoperable with RDF triple syntax (subject, predicate, object), facilitating its use in knowledge graphs (David I. Spivak and Kent 2012).
Planning using \(\catSet{C}\) and DPO Rewriting
Existing state-space planning algorithms can be adapted to work with this planning representation.
Example: ForwardPlan() executes depth-first search (DFS) to find a sequence of actions.
function ForwardPlan(world::ACSet, goal::ACSet, actions::Dict,
action_limits::Dict, action_usage::Dict,
plan::List)
# Exit criteria: goal is reached if there is a monic morphism from goal to world
if homomorphism(goal, world, monic=true) !== nothing
println("Goal reached.")
return plan
end
# Find applicable actions for the current world state
applicable = find_applicable_actions(world, actions)
# Backtrack criteria: no applicable actions
if length(applicable) <= 0
throw("No applicable actions found! Terminate path...")
end
# Iterate over all applicable actions
for action in applicable
action_name = action.first
match_morphism = action.second
# Backtrack criteria: action applied too many times
try
if action_usage[action_name] >= action_limits[action_name]
println("Abort path. Action used too many times.")
continue
end
catch
# Initialize action usage if it doesn't exist
action_usage[action_name] = 1
end
# Save current world state for backtracking
prev_world = world
selected_action = action[action_name].rule
# Apply the selected action to the current world state
try
world = rewrite(selected_action, world)
catch e
throw("Could not apply action!")
end
# Record the action and corresponding match morphism in the current plan
append!(plan, [selected_action => match_morphism])
try
# Recursively call ForwardPlan with updated world state
plan = ForwardPlan(world, goal, actions, action_limits,
action_usage, plan)
return plan
catch e
# Backtrack to previous world state if path fails
world = prev_world
pop!(plan)
println("Path failed. Try a different path.")
end
end
# If no valid plan is found, report failure
println("No plan found.")
endTransfer using Functorial Data Migration, \(\Delta_F\)
High-level Steps in Analogical Plan Transfer
- Define the Source Domain: Start by defining the ontology, \(\cat{D}_S\), and actions, \(A_S\), for the source domain, \(\textbf{D}_S\).
- Define the Planning Problem: Establish the initial and goal states, \(P_S = (I, G)\) within domain \(\textbf{D}_S\).
- Plan: Solve for a valid plan, \(\pi_S\), that solves for \(P_S\) within domain \(\textbf{D}_S\).
- Define the Target Domain Ontology: Specify the target ontology, \(\cat{D}_T\), in the new domain, \(\textbf{D}_T\).
- Align Ontologies: Create a translation map, \(F: \cat{D}_T \rightarrow \cat{D}_S\), linking the types and predicates from the target domain ontology to the source domain ontology.
- Transfer the Plan: Use the translation map to transfer the grounded plan via \(\Delta_F\), resulting in \(\pi_T\).
- Validate the Plan: Check that the end state after \(\pi_T\) contains \(\Delta_F(G)\).
Stacking Blocks \(\sim\) Making a Sandwich
Kitchenworld ontology derived from AI2-Thor Object Type Documentation
(Allen Institute for Artificial Intelligence 2024)
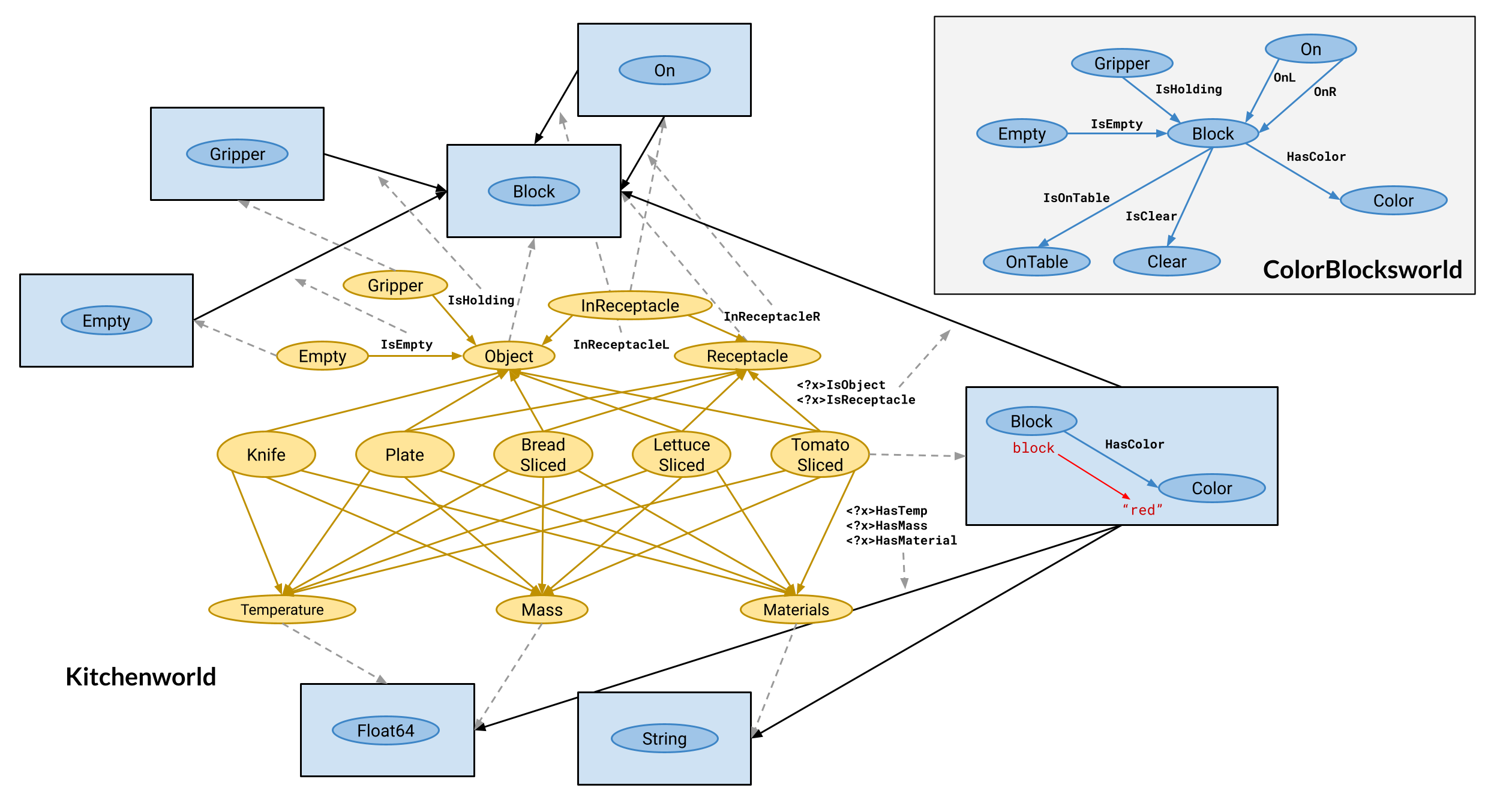
Uses an ontology alignment map that is functorial
Result
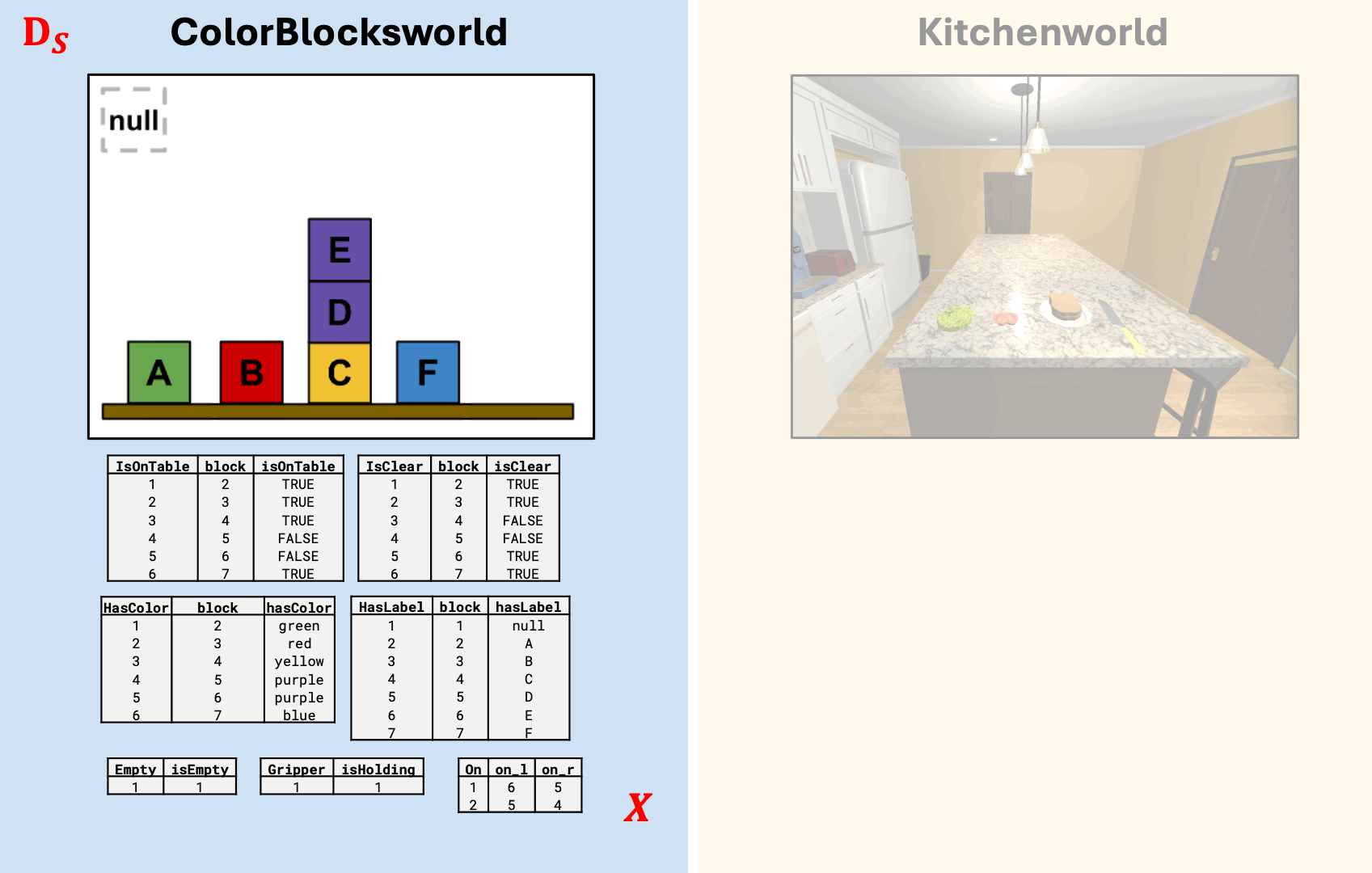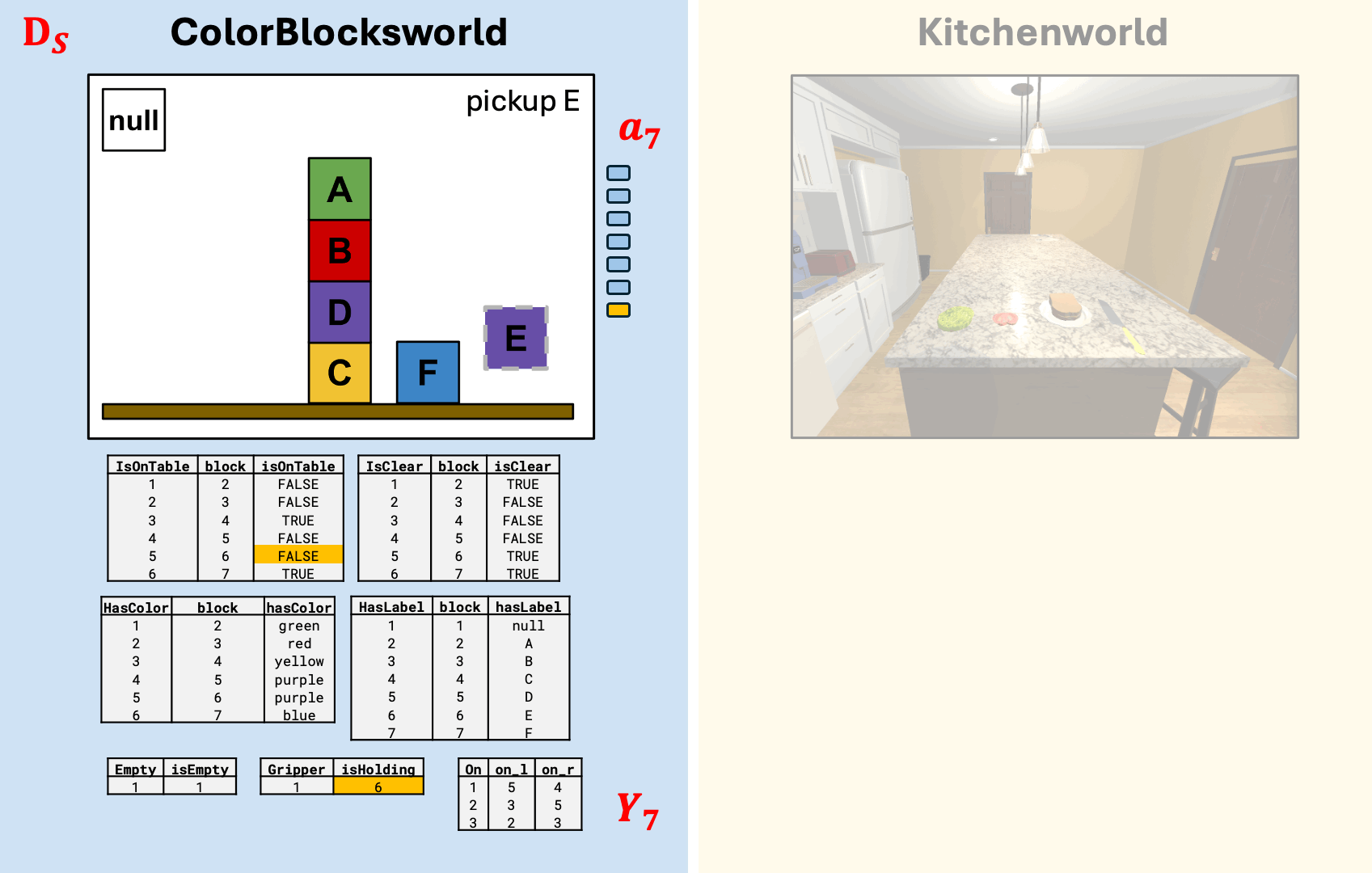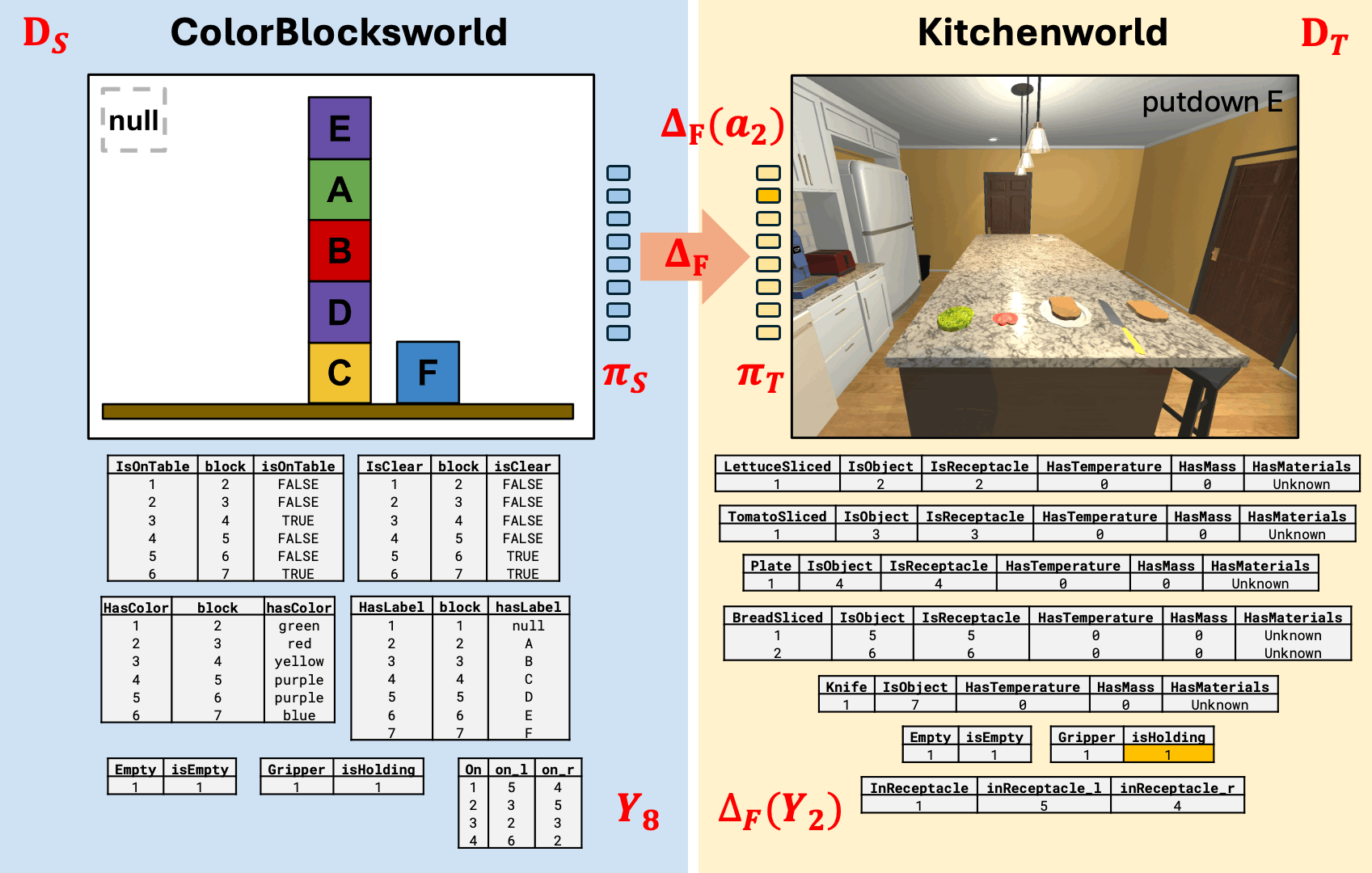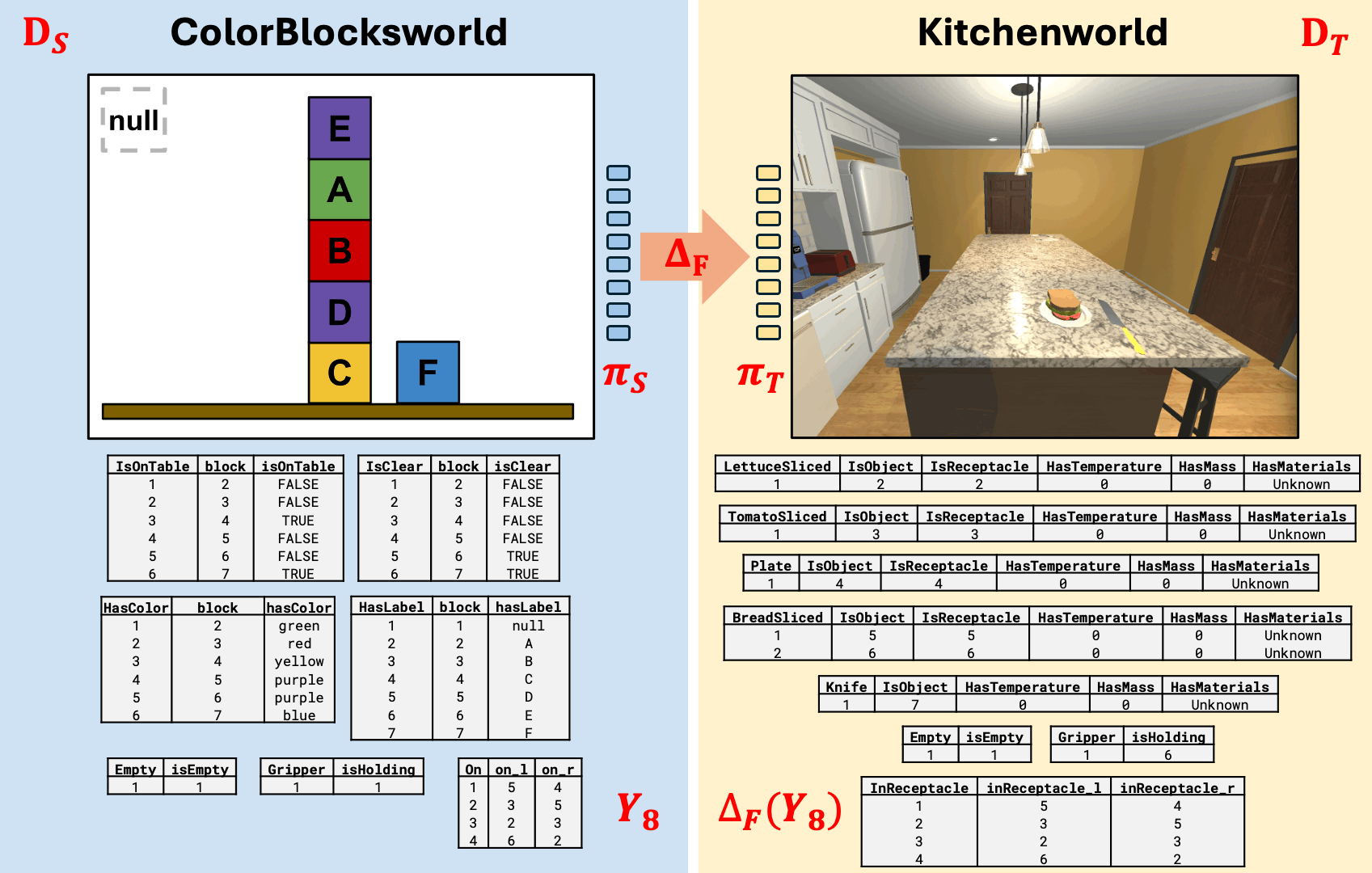
Kitchenworld simulation from AI2-Thor (Allen Institute for Artificial Intelligence 2024)
Advantages and Limitations of Categorical Structure for Planning
Advantages
- Preserves ontological structure when applying actions and transferring plans
- Predictable runtime complexity w.r.t. PDDL and its extensions, e.g. typing and transitive closure constraints
- Generalized transfer for pair of domains
- Symbolic action (skill) generation
Limitations
- Reliance on advanced mathematical theory
- Higher runtime complexity for checking applicability of actions, \(O(n^k)\), w.r.t. PDDL, \(O(nk)\)
- Depends on proper (functorial) ontological alignment
- Difficulty handling structurally dissimilar domains
Areas of Future Work
Scaling Studies: Empirical and Theoretical
- More planning and plan transfer problems
- Scale by the size of the world state and ontology
- Scale by length of plan
- Design benchmarks, e.g. transfer accuracy
- Study functoriality of migration for certain ontology maps
A Software Tool for Category Theory-Based Planning and Transfer
- Run planners
- Automate discovery of functorial ontology alignments
- Perform analogical plan transfer
- Compose plans with other plans using sequential transfer
- Check plans satisfy abstract behavior using hierarchical transfer
Knowrob (Tenorth and Beetz 2017) and Factory of the Future (Schäfer et al. 2021) ontologies
What is category theory?
Category theory (Eilenberg and MacLane 1945) is often referred to as the “mathematics of mathematics”.
Connects different areas of mathematics by studying the relationships between structures.
Category theory has been applied in many domains outside mathematics1, and such works contribute to the field of Applied Category Theory (ACT).
Definition: (Category) A category, \(\cat{C}\), consists of:
- a collection of objects, \(\text{Ob}(\cat{C})\)
- a collection of morphisms for every pairs of objects, \(\text{Hom}_\cat{C}(X,Y)\) for \(X, Y \in \text{Ob}(\cat{C})\)
- a composition operation, if \(f: X \rightarrow Y\), \(g: Y \rightarrow Z\) then \(g \circ f: X \rightarrow Z\)
- an identity morphism for every object, \(1_X: X \rightarrow X\)
satisfying the associativity law \(h \circ (g \circ f) = (h \circ g) \circ f\) and unitality laws \(f \circ 1_x = f\) and \(1_y \circ f = f\) whenever these equations make sense.
Functors and natural transformations
Functors map, e.g. \(\; F: \cat{P(\{1,2\})} \rightarrow \cat{\mathbb{N}_{\leq}}\):
- Objects to objects
- Morphisms to morphisms
- Preserves composition in the source category
Functors and natural transformations
Functors map, e.g. \(\; F: \cat{P(\{1,2\})} \rightarrow \cat{\mathbb{N}_{\leq}}\):
- Objects to objects
- Morphisms to morphisms
- Preserves composition in the source category
Natural transformations map functors, e.g. \(\alpha: F \rightarrow G\):
- Defines morphism in target category, \(\cat{\mathbb{N}_{\leq}}\), per object in source category, e.g. \(\cat{P(\{1,2\})}\)
- Preserves composition in the source category
References
