using Catlab
using AlgebraicRewriting
@present OntColorBlocksworld(FreeSchema) begin
# Types
Block::Ob
Empty::Ob
Gripper::Ob
HasColor::Ob
IsClear::Ob
IsOnTable::Ob
HasLabel::Ob
Color::AttrType
Clear::AttrType
OnTable::AttrType
Label::AttrType
# Predicates
isEmpty::Hom(Empty, Block)
isHolding::Hom(Gripper, Block)
hasColor::Attr(HasColor, Color)
hasColorDom::Hom(HasColor, Block)
isClear::Attr(IsClear, Clear)
isClearDom::Hom(IsClear, Block)
isOnTable::Attr(IsOnTable, OnTable)
isOnTableDom::Hom(IsOnTable, Block)
hasLabel::Attr(HasLabel, Label)
hasLabelDom::Hom(HasLabel, Block)
# Relations
On::Ob
onL::Hom(On, Block)
onR::Hom(On, Block)
end
# Create a C-set type based on ontology
@acset_type ColorBlocksworld(OntColorBlocksworld)Sequential, Hierarchical, and Analogical
Plan Transfer in Robotics
Doctoral Defense
Department of Computer Science
University of Maryland, College Park
December 2, 2024
About Me
Ph.D. Candidate in Computer Science at University of Maryland, College Park
- Since 2018
- Topos Institute (Research Associate), NIST, Siemens
Research Staff Member at the Johns Hopkins University Applied Physics Laboratory
- Since 2017
- Sponsors: CDC, NASA, FEMA, Army National Guard, …
Previously B.S. and M.S. Electrical Engineering from Drexel University in Philadelphia, PA in 2017



\[ \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\cat}[1]{\mathsf{#1}} \newcommand{\CAT}[1]{\mathsf{#1}} \newcommand{\Set}{\CAT{Set}} \DeclareMathOperator{\Path}{Path} \newcommand{\catSet}[1]{\cat{#1}\text{-}\Set} \DeclareMathOperator{\Ob}{Ob} \DeclareMathOperator{\Hom}{Hom} \]
Structure of the talk
- Motivation for the Research
- Current Approaches and Gaps
- My Research
- Deep Dive: Analogical Plan Transfer
- Future Work and Conclusion
Follow along!
Motivation for the Research
An example of plan transfer, goals of the dissertation, and the bigger picture
Let’s take an example
Agility Robotics (left) and Brightpick Robot (right) showcased during ProMat 2023
Humanoid robot
Arms
Bins
Conveyer Belt
Mobile robot
Lift
Box
Problem: Designing planning problems and running planners is time-consuming.
(Alnazer and Georgievski 2023) (Ingrand and Ghallab 2017)
What do I mean by transferring plans?
- Transfers whole plans or individual actions
- Can be executed in sequence with other plans
- Preserves high-level behavior
- Can be adapted to a new environment
Goals of this dissertation
Provide a:
Conceptual framework
vocabulary used to describe types of transfers
Mathematical framework
system to validate whether each type of transfer is successful
Case studies
examples demonstrating the effectiveness of the mathematical framework
for task plan transfer, or plan transfer, in robotics.
Potential Applications

Interoperability in Mission Planning
Transferring the course of action (CoA) for a supply distribution plan from one disaster scenario to another.

Standards and Privacy in Manufacturing
Transferring an abstract, standardized plan and adapting it with manufacturer-specific details
Section 8.4 in (Aguinaldo 2024)
Current Approaches and Gaps
Plan transfer in robotics, the gaps, and foundations of category theory
What is planning in robotics?
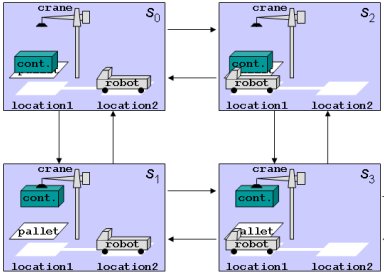
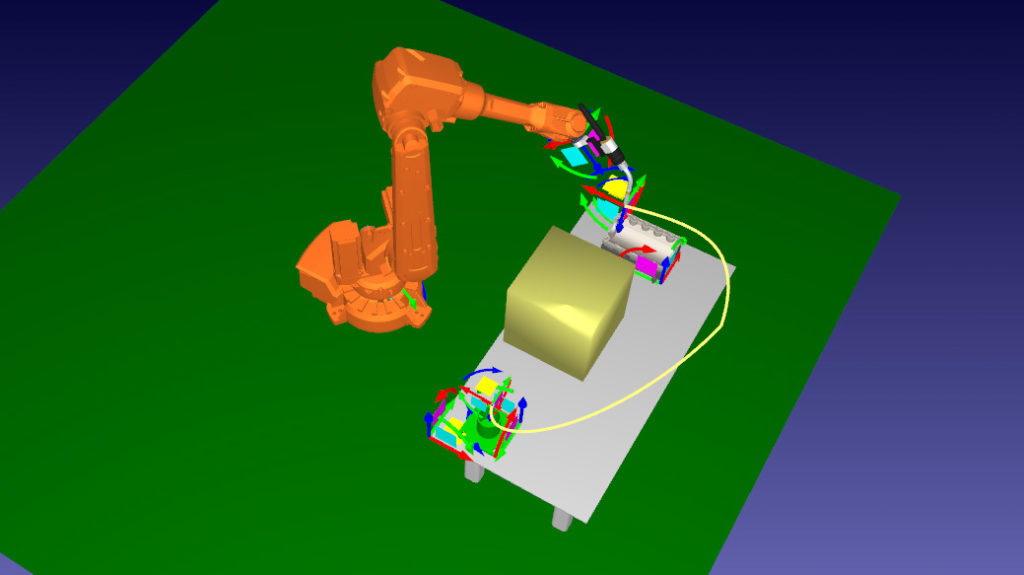
Task Planning
Motion Planning
Abstract decision-making
Symbolic states
Discrete action space
Algorithmic search
AI Planning
Physical maneuver
Geometric states
Continuous configuration space
Robot kinematics and dynamics
Robotics
1970s - 2000s
Image creds: Gerhard Wickler (task), RoboDK (motion)
What is planning in robotics?


Task Planning
Motion Planning
Abstract decision-making
Symbolic states
Discrete action space
Algorithmic search
AI Planning
Physical maneuver
Geometric states
Continuous configuration space
Robot kinematics and dynamics
Robotics
(after 2010) Task and Motion Planning (TAMP)
Coordinating high-level and low-level planning
(Kaelbling and Lozano-Pérez 2011), (Garrett et al. 2021), (Mansouri, Pecora, and Schüller 2021)
Image creds: Gerhard Wickler (task), RoboDK (motion)
What is plan transfer in robotics? (today)
Transfer learning is the process of reusing knowledge, e.g. models, trained in one domain in another domain:
- feature spaces or distributions in machine-learning (Pan and Yang 2009)
- state or action spaces in reinforcement learning (RL) (Taylor and Stone 2009)
- robot (embodiment), task, or environment in robotics (Jaquier et al. 2023)
Some techniques in robotics include:
learning a shared feature space across different environments (universal domain adaptation),
learning multiple tasks at once (RL meta-learning), and
learning mapping between different kinematic structures (motion retargeting).
Chapter 2 in (Aguinaldo 2024)
What’s the gap?
1. Plan transfer in robotics typically focuses on motion planning, neglecting task-level transfer at the symbolic representation.
CONTRIBUTION 1: Focus on task-level transfer.
2. Current approaches lack flexibility in broader transfer use cases, such as partial plan transfer or integrating plans into larger behaviors.
CONTRIBUTION 2: Identify broader transfer uses cases. The way robot programming has evolved gives a hint to how humans aim to reuse existing robot behaviors.
3. There lacks standardized frameworks to formally evaluate the success of plan transfer.
CONTRIBUTION 3: Establish a formal framework that can account for all types of transfer. Category theory, with its emphasis on abstraction and compositionality, is a good candidate for this mathematical framework.
Contributions of this Dissertation
1. Plan transfer in robotics typically focuses on motion planning, neglecting task-level transfer at the symbolic representation.
CONTRIBUTION 1: Focus on task-level transfer.
2. Current approaches lack flexibility in broader transfer use cases, such as partial plan transfer or integrating plans into larger behaviors.
CONTRIBUTION 2: Identify broader transfer uses cases. The way robot programming has evolved gives a hint to how humans aim to reuse existing robot behaviors.
3. There lacks standardized frameworks to formally evaluate the success of plan transfer.
CONTRIBUTION 3: Establish a formal framework that can account for all types of transfer. Category theory, with its emphasis on abstraction and compositionality, is a good candidate for this mathematical framework.
What is category theory?
Category theory (Eilenberg and MacLane 1945) is often referred to as the “mathematics of mathematics”.
Connects different areas of mathematics by studying the relationships between structures.
Category theory has been applied in many domains outside mathematics1, and such works contribute to the field of Applied Category Theory (ACT).
Definition: (Category) A category, \(\cat{C}\), consists of:
- a collection of objects, \(\text{Ob}(\cat{C})\)
- a collection of morphisms for every pairs of objects, \(\text{Hom}_\cat{C}(X,Y)\) for \(X, Y \in \text{Ob}(\cat{C})\)
- a composition operation, if \(f: X \rightarrow Y\), \(g: Y \rightarrow Z\) then \(g \circ f: X \rightarrow Z\)
- an identity morphism for every object, \(1_X: X \rightarrow X\)
satisfying the associativity law \(h \circ (g \circ f) = (h \circ g) \circ f\) and unitality laws \(f \circ 1_x = f\) and \(1_y \circ f = f\) whenever these equations make sense.
Chapter 3 in (Aguinaldo 2024)
Functors and natural transformations
Functors map, e.g. \(\; F: \cat{P(\{1,2\})} \rightarrow \cat{\mathbb{N}_{\leq}}\):
- Objects to objects
- Morphisms to morphisms
- Preserves composition in the source category
Chapter 3 in (Aguinaldo 2024)
Functors and natural transformations
Functors map, e.g. \(\; F: \cat{P(\{1,2\})} \rightarrow \cat{\mathbb{N}_{\leq}}\):
- Objects to objects
- Morphisms to morphisms
- Preserves composition in the source category
Natural transformations map functors, e.g. \(\alpha: F \rightarrow G\):
- Defines morphism in target category, \(\cat{\mathbb{N}_{\leq}}\), per object in source category, e.g. \(\cat{P(\{1,2\})}\)
- Preserves composition in the source category
Chapter 3 in (Aguinaldo 2024)
Monoidal Categories and String Diagrams
Informal Definition: (Monoidal Category)
A monoidal category, \(\cat{M}\), consists of:
- a collection of objects, \(\text{Ob}(\cat{M})\)
- a collection of morphisms for every pairs of objects, \(\text{Hom}_\cat{M}(X,Y)\) for \(X, Y \in \text{Ob}(\cat{M})\)
- a composition operation, if \(f: X \rightarrow Y\), \(g: Y \rightarrow Z\) then \(g \circ f: X \rightarrow Z\)
- an identity morphism for every object, \(1_X: X \rightarrow X\)
- a monoidal product, \(\otimes: \cat{M} \times \cat{M}\)
- a unit object, \(1 \in \cat{M}\)
satisfying the associativity law \(h \circ (g \circ f) = (h \circ g) \circ f\) and unitality laws \(f \circ 1_x = f\) and \(1_y \circ f = f\) whenever these equations make sense.
other laws…
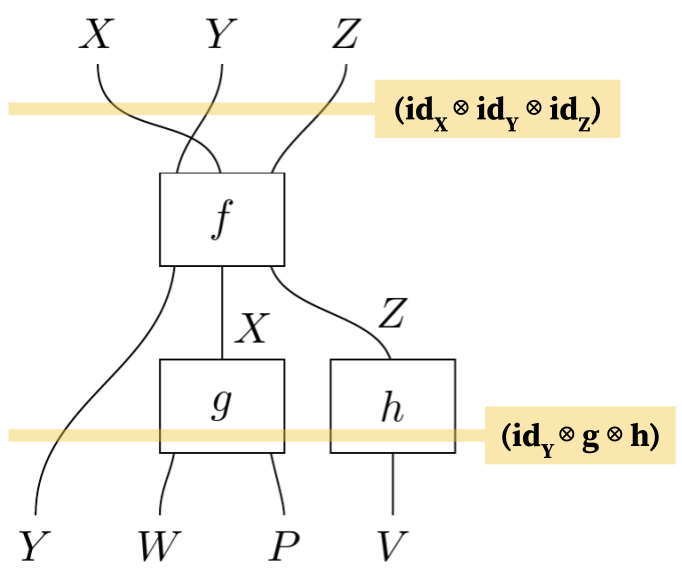
An example string diagram
(Master et al. 2020), (Abramsky and Coecke 2008), (Selinger 2010), (Breiner, Jones, and Subrahmanian 2016)
Chapter 3 in (Aguinaldo 2024)
My Research
My conceptual framework, mathematical framework, and case studies
My conceptual framework for plan transfer
Sequential Transfer
Like motion primitives and skills (Bøgh et al. 2012), (Ionescu 2020), (Proctor et al. 2016), Section 2.2 in (Aguinaldo 2024)
- Valid composition
- Same planning domain
Hierarchical Transfer
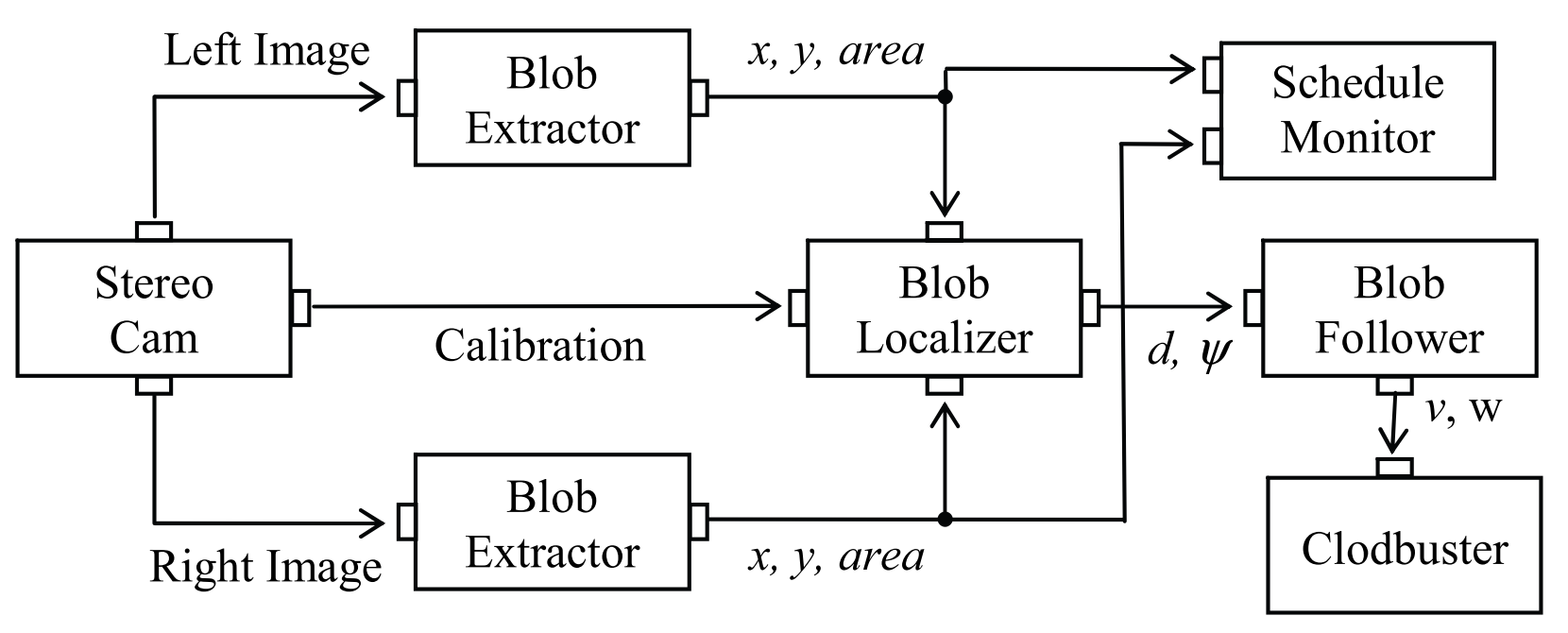
Like modular architectures (Cowley, Chaimowicz, and Taylor 2006) and middlewares (Aragão, Moreno, and Bernardino 2016), (Yang Liang 2008), (Matai et al. 2008), Section 2.3 in (Aguinaldo 2024)
- Preserves composition and abstract behavior
- Same planning domain
Analogical Transfer
Like robot program translation (Freund et al. 2001), (Freund and Luedemann-Ravit 2002), (Adam et al. 2017), (Ringert et al. 2014), (Souza et al. 2019), (Carvalho de Souza et al. 2020), Section 2.4 in (Aguinaldo 2024)
- Achieves analogous goal state
- Different planning domain
Chapter 1 in (Aguinaldo 2024)
My mathematical framework and case studies
Sequential Transfer
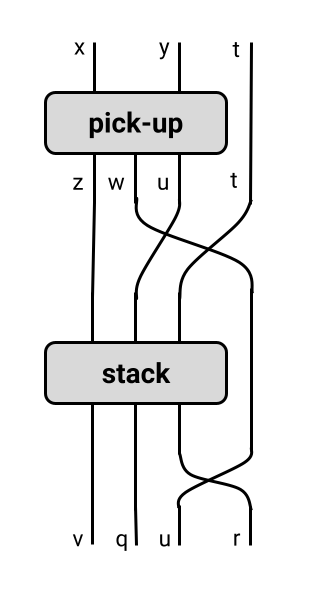
Key Insight: Propagate preconditions and effects to check plan composition
Tools: Symmetric monoidal categories (SMCs) (Joyal and Street 1991) and string diagrams (Marsden 2014)
Chapter 4 in (Aguinaldo 2024)
Hierarchical Transfer

Key Insight: Use functors to map high-level task abstractions to low-level abstractions
Tools: SMCs, monoidal functors, and functors (Leinster 2016)
Chapter 5 in (Aguinaldo 2024)
Analogical Transfer
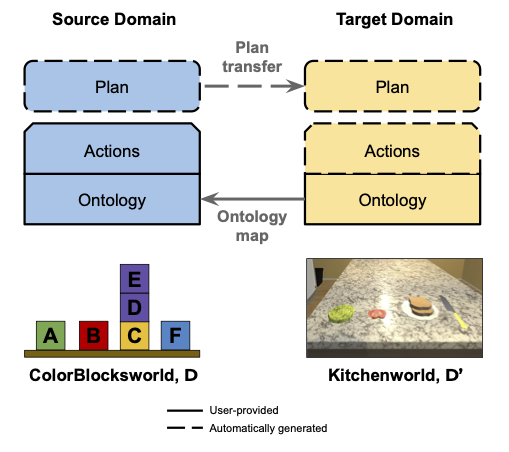
Key Insight: Transfer whole plans using an ontological map between planning domains
Tools: \(\cat{C}\)-sets (David I. Spivak and Kent 2011), (Patterson, Lynch, and Fairbanks 2021), DPO rewriting (K. Brown et al. 2023), and functorial data migrations (David I. Spivak and Kent 2012)
Chapter 6 & 7 in (Aguinaldo 2024)
Sequential Transfer: An Overview
Strings diagrams can propagate preconditions and effects of actions in a plan to check plan composition. (Aguinaldo and Regli 2021)
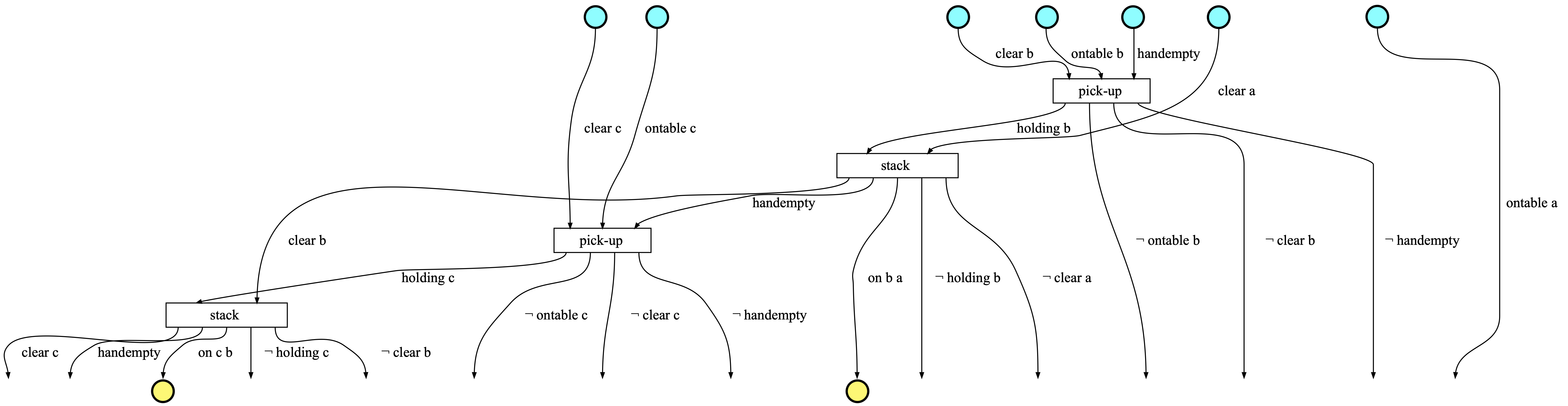
| State | World State | Action |
|---|---|---|
| Initial | clear c, ontable c, clear b, ontable b, handempty, clear a, ontable a | |
| Step 1 | clear c, ontable c, clear b, ontable b, handempty, clear a, ontable | pick-up |
| Step 2 | clear c, ontable c, holding b, clear a, ¬ontable b, ¬clear b, ¬handempty, ontable a | stack |
| Step 3 | clear b, clear c, ontable c, handempty, on b a, ¬holding b, ¬clear a, ¬ontable b, ¬clear b, ¬handempty, ontable a | pick-up |
| Step 4 | holding c, clear b, ¬ontable c, ¬clear c, ¬handempty, on b a, ¬holding b, ¬clear a, ¬ontable b, ¬clear b, ¬handempty, ontable a | stack |
| Goal | clear c, handempty, on c b, ¬holding c, ¬clear b, ¬ontable c, ¬clear c, ¬handempty, on b a, ¬holding b, ¬clear a, ¬ontable b, ¬clear b, ¬handempty, ontable a |
Chapter 4 in (Aguinaldo 2024)
Hierarchical Transfer: An Overview
The categories \(\cat{Task}\), \(\cat{Virtual}\), \(\cat{Motion}\) are defined. Functors,
\(F: \cat{Task} \rightarrow \cat{Virtual} \quad \quad G: \cat{Virtual} \rightarrow \cat{Motion}\)
can be used to guarantee that the structure in \(\cat{Task}\) is preserved. (Aguinaldo et al. 2021)
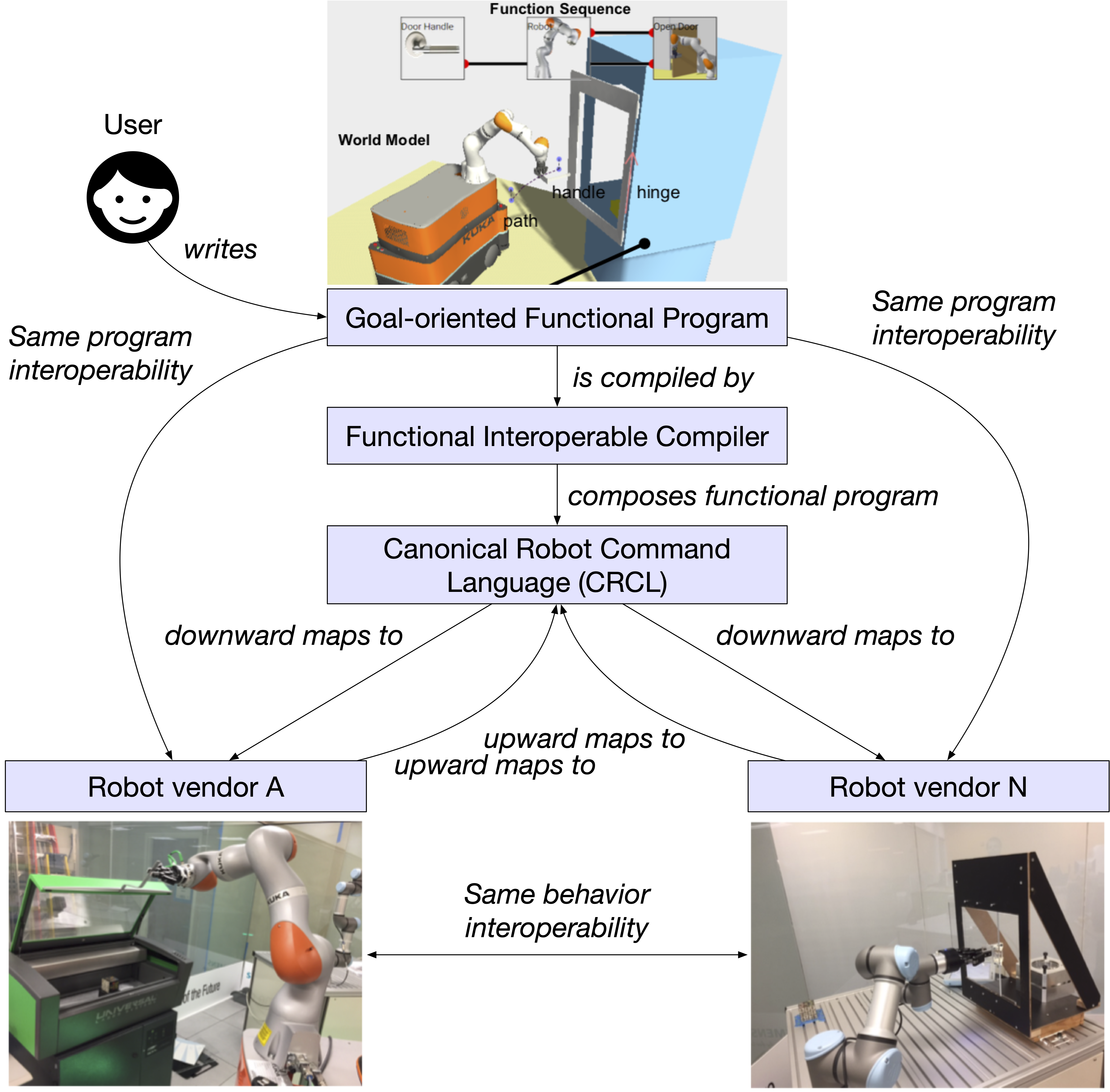
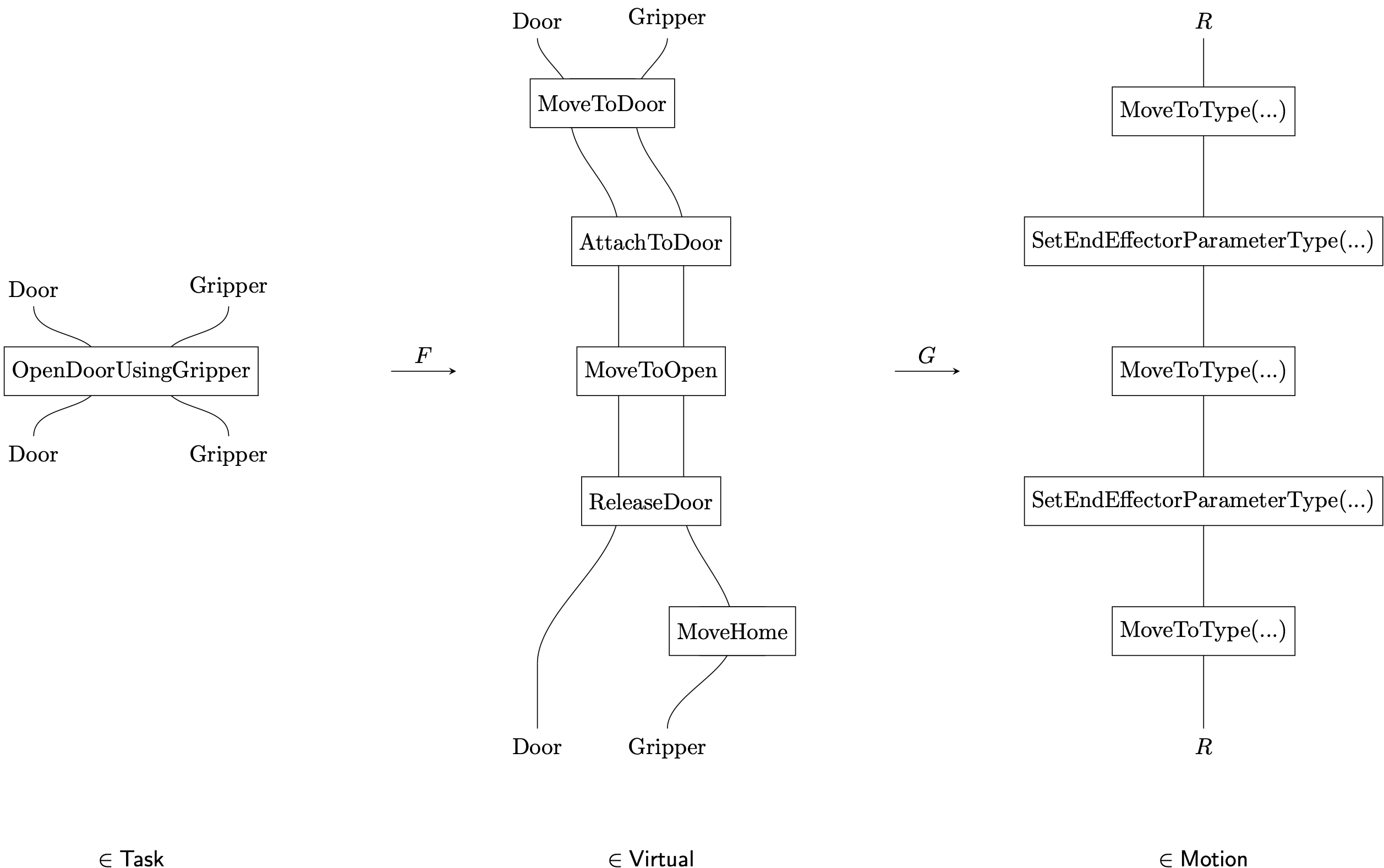
Chapter 5 in (Aguinaldo 2024)
Analogical Plan Transfer: A Deep Dive
How it works and a new planning representation language
What can we do with analogical plan transfer?
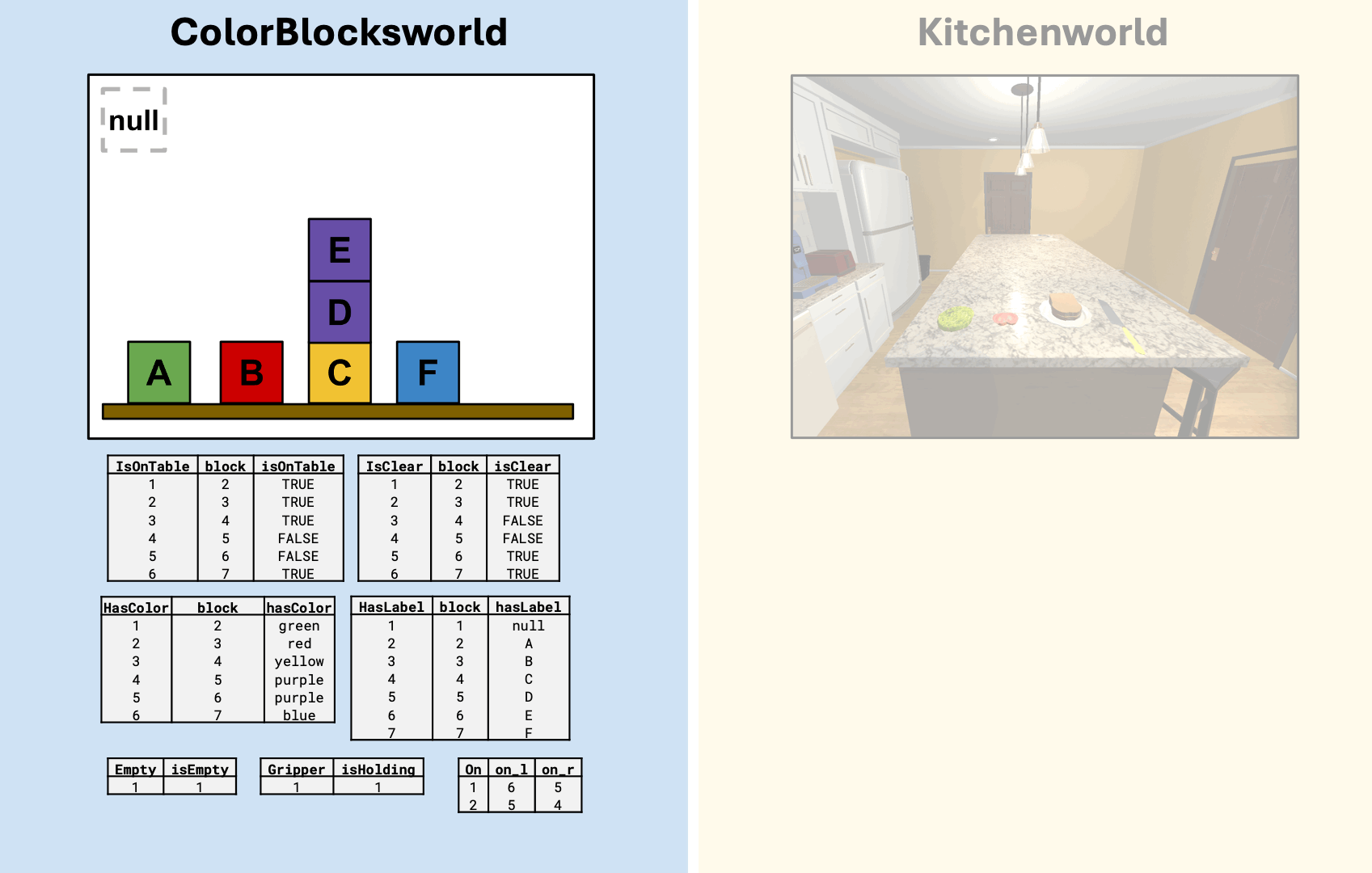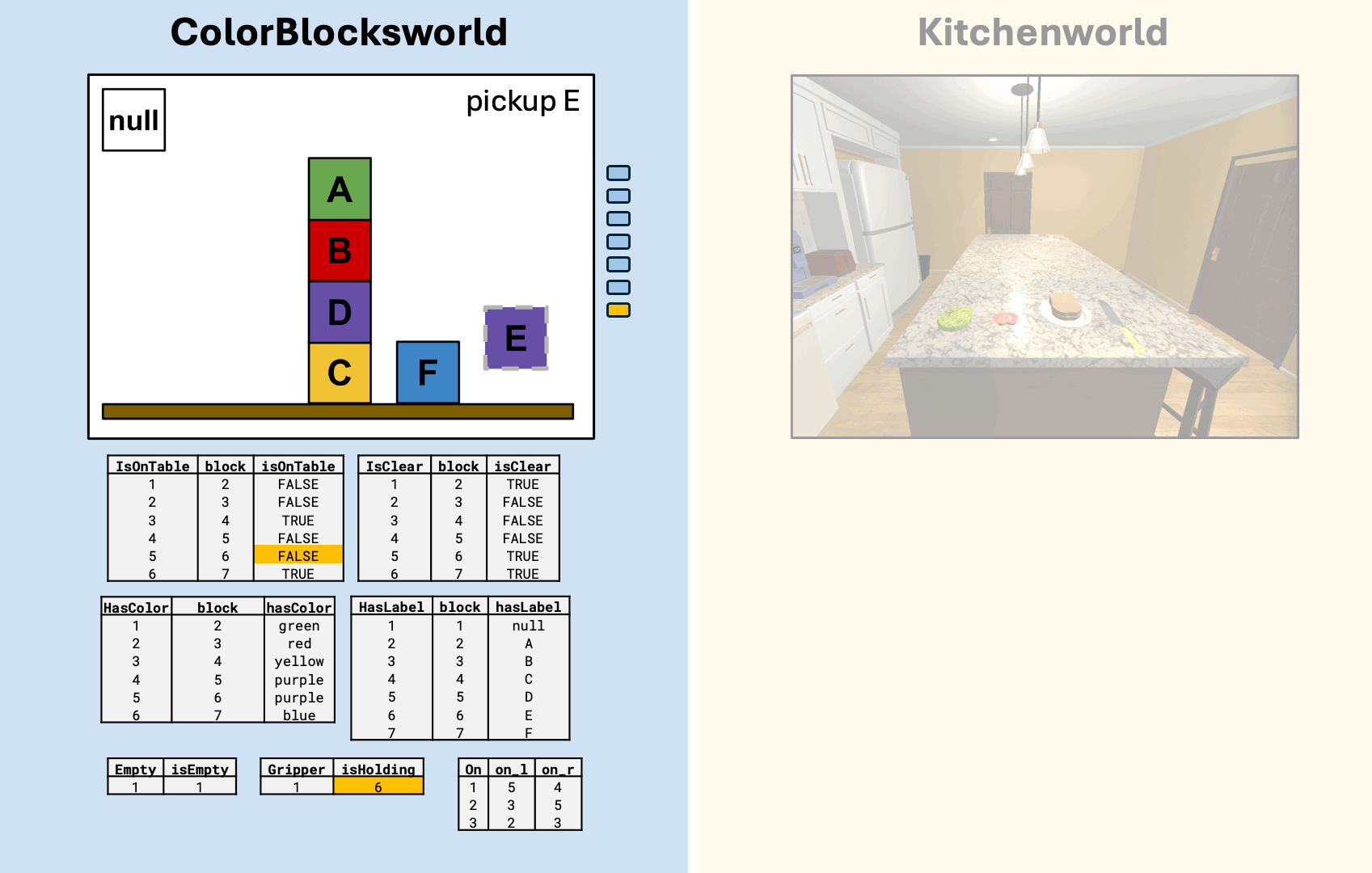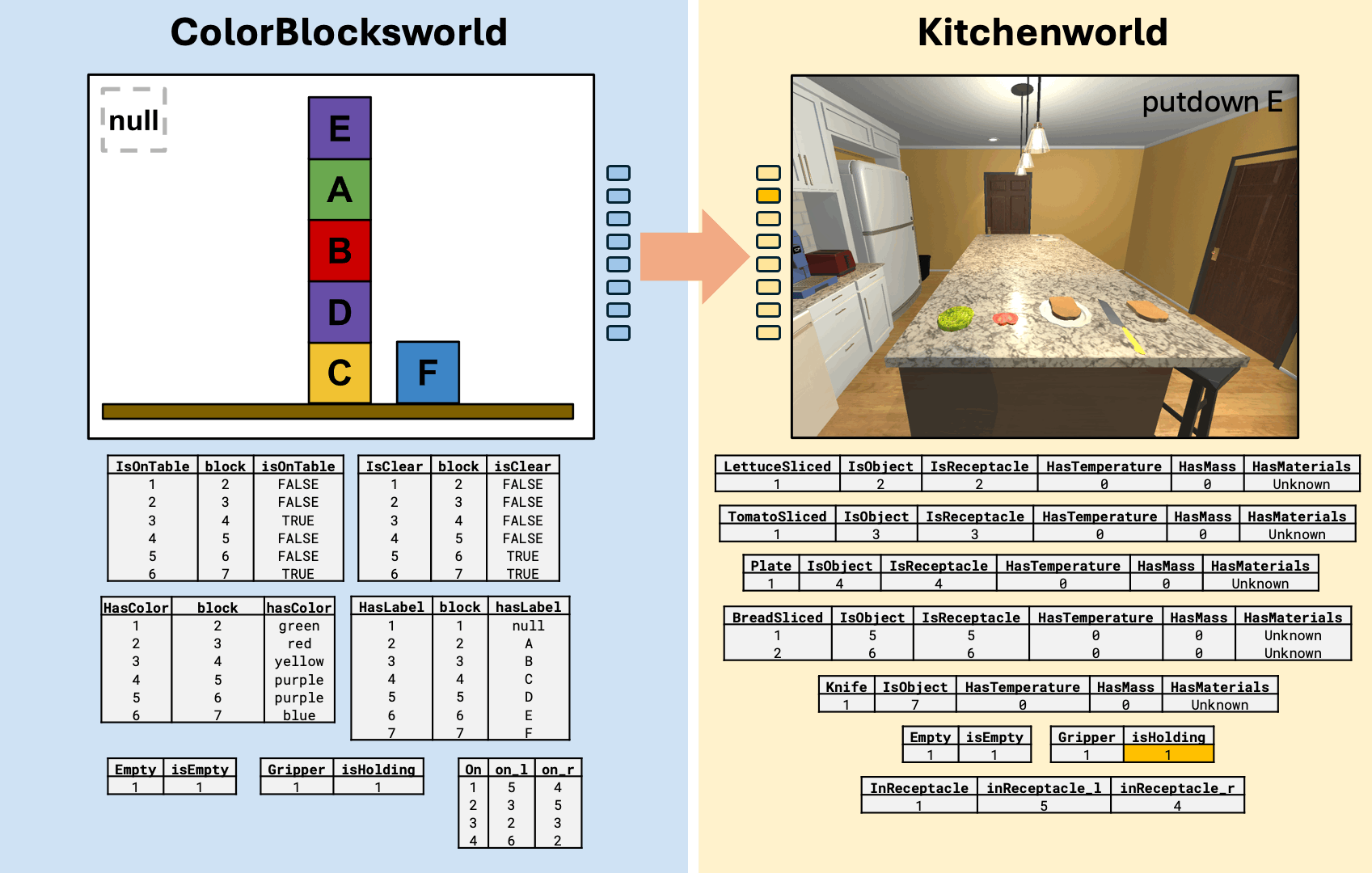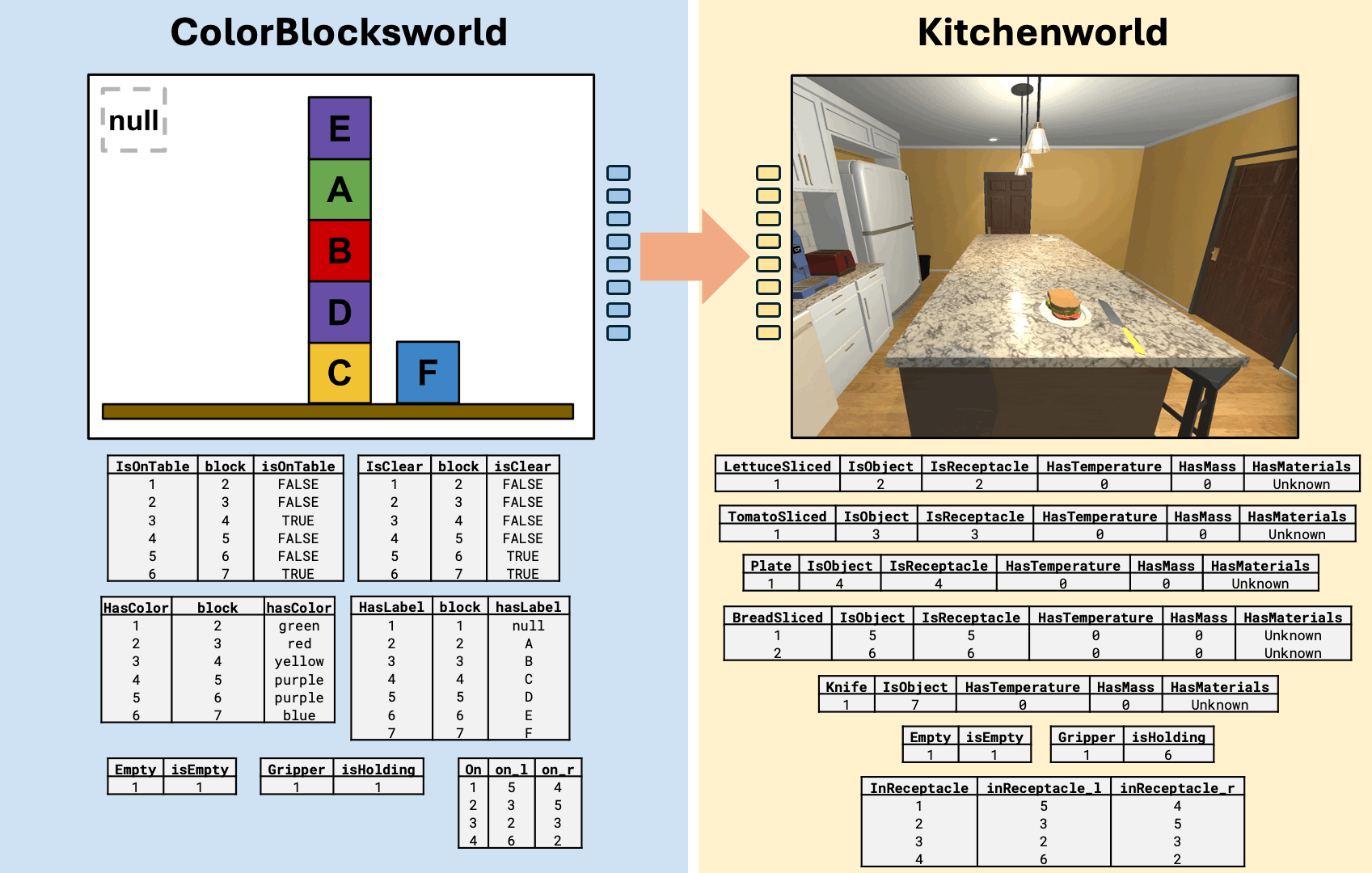
Kitchenworld simulation from AI2-Thor (Allen Institute for Artificial Intelligence 2024)
Why does this work?
Kitchenworld ontology derived from AI2-Thor Object Type Documentation
(Allen Institute for Artificial Intelligence 2024)
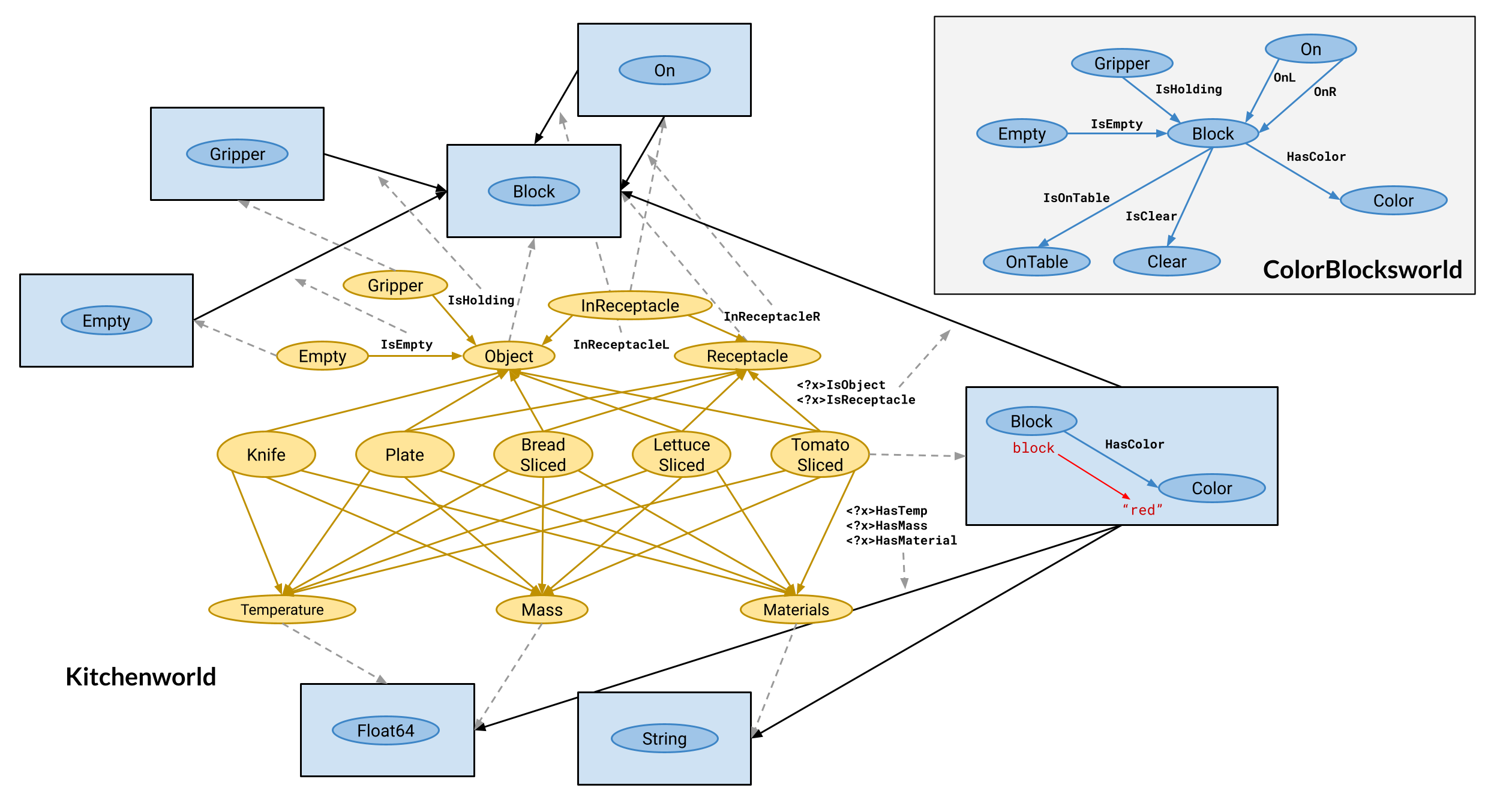
Uses an ontology alignment map that is functorial
Section 7.7 in (Aguinaldo 2024)
Formal Theory of Analogies
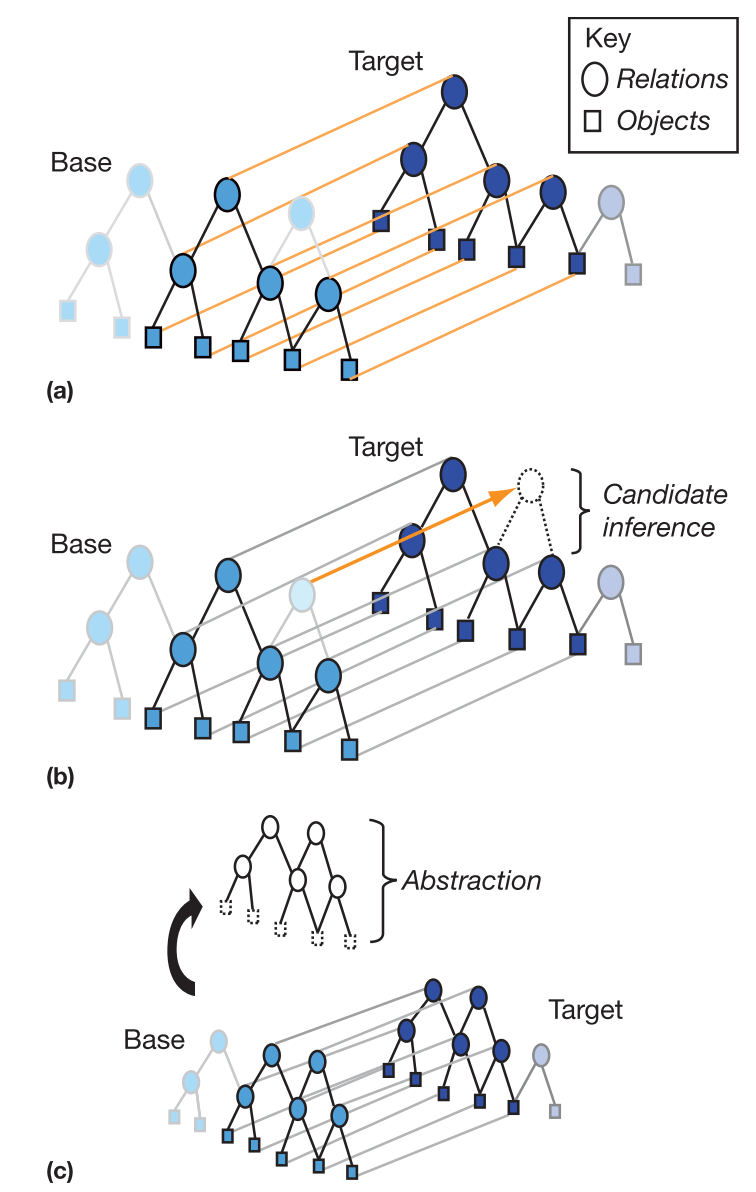
(Gentner and Smith 2012)
Why analogies?
(Wilkins and DesJardins 2001) argued that an ideal system should mimic human behavior by using analogies to transfer solutions from one problem to another.
What are analogies?
According to (Gentner 1983), analogies:
- have a one-to-one correspondence, each concept in the source domain maps to at most one concept in the target domain
- adhere to the systematicity principle, where analogical maps connect large, densely connected systems of concepts, instead of just a handful of isolated concepts
Definition: (Analogical Transfer) Analogical transfer involves identifying structural similarities, or analogies, between planning domains and leveraging these analogies to adapt plans from one context to another. (Aguinaldo 2024)
Chapter 7 in (Aguinaldo 2024)
Analogies with Task Planning
PDDL1 does not have built-in support for domain comparison or domain ontology alignment. Therefore, a new planning language that supports these capabilities is a prerequisite for analogical plan transfer. (Aguinaldo 2024)
State Transition System Model for Planning
- States, \(S = \{s_0, s_1, s_2, \dots\}\) set of all possible states
- Actions, \(A = \{a_0, a_1, a_2, \dots\}\) set of all possible actions
- Preconditions, \(\mathrm{Pre}(a)\) conditions that must be true in the state for the action to be applied
- Effects, \(\mathrm{Eff}(a)\) conditions are true in the state after the action is applied
- Transition function, \(\gamma: A \times S \rightarrow S\) partial function that maps an action and a state to the resulting state
- Checking applicability an action \(a \in A\) is at state \(s \in S\) if \(\gamma(a, s)\) is defined
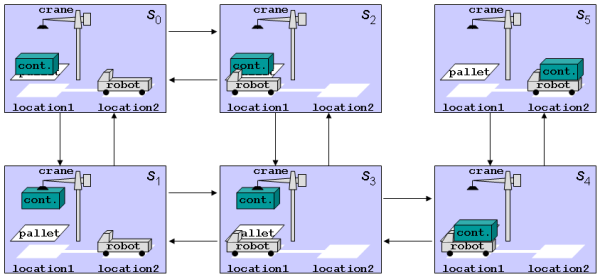
Chapter 6 in (Aguinaldo 2024)
Planning States as \(\cat{C}\)-sets
Definition: (\(\cat{C}\)-set, schema category) A \(\cat{C}\)-set is a functor from \(\cat{C} \rightarrow \cat{Set}\). \(\cat{C}\) is referred to as the schema category (i.e. ontology). \(\cat{Set}\) is a category whose objects are sets and whose morphisms are set function maps.
Example (Section 6.4.1 in (Aguinaldo 2024)):
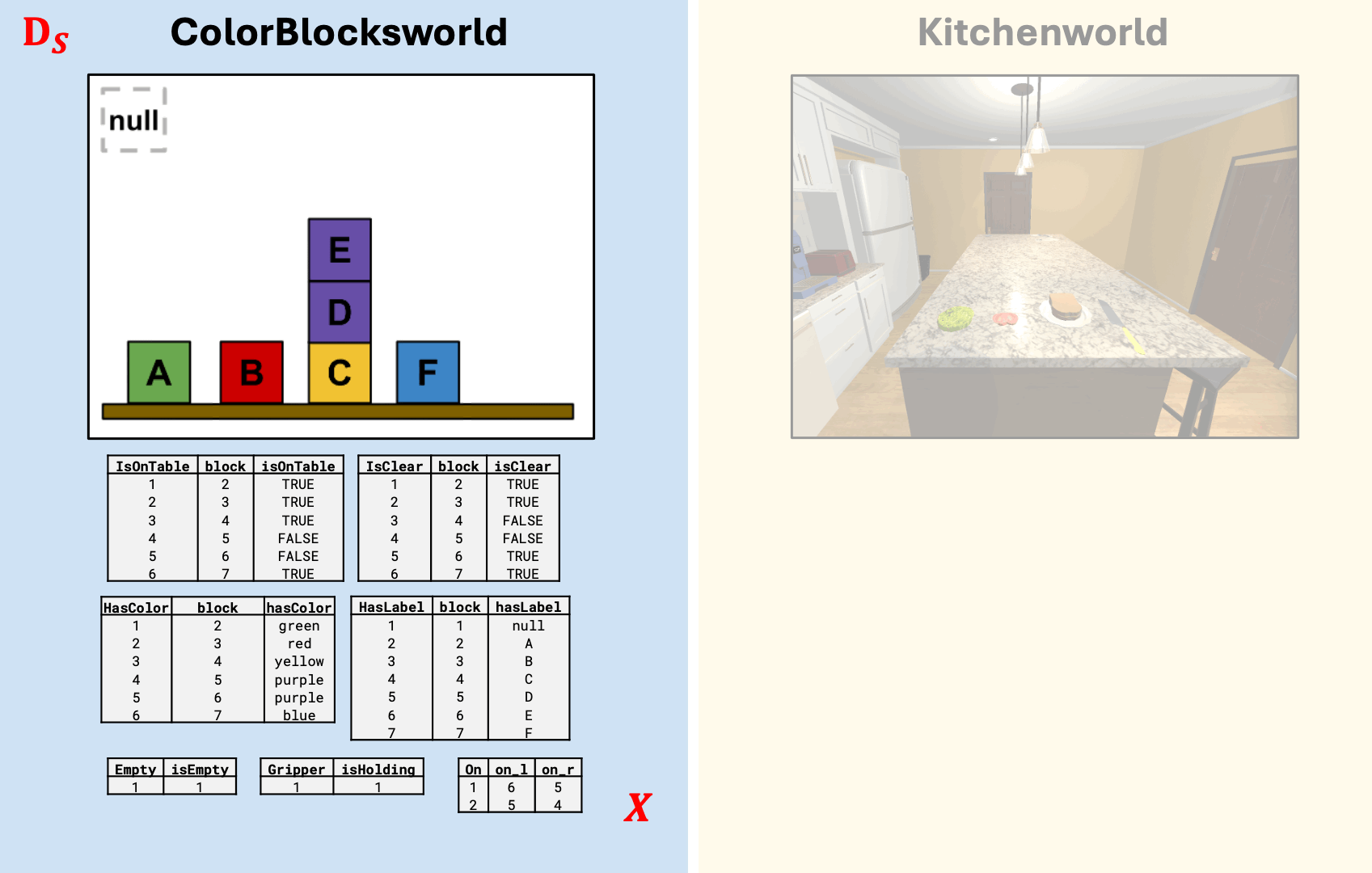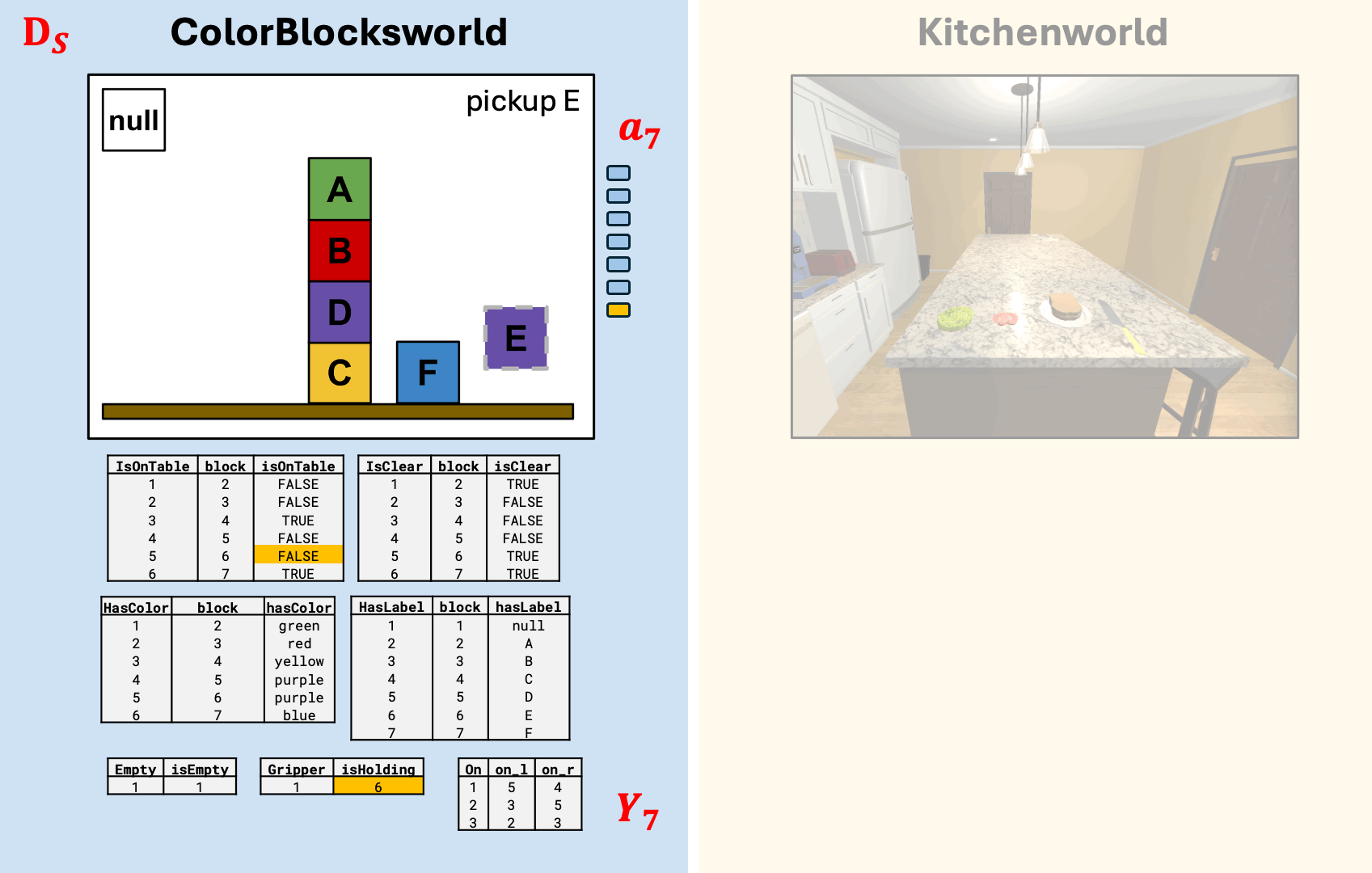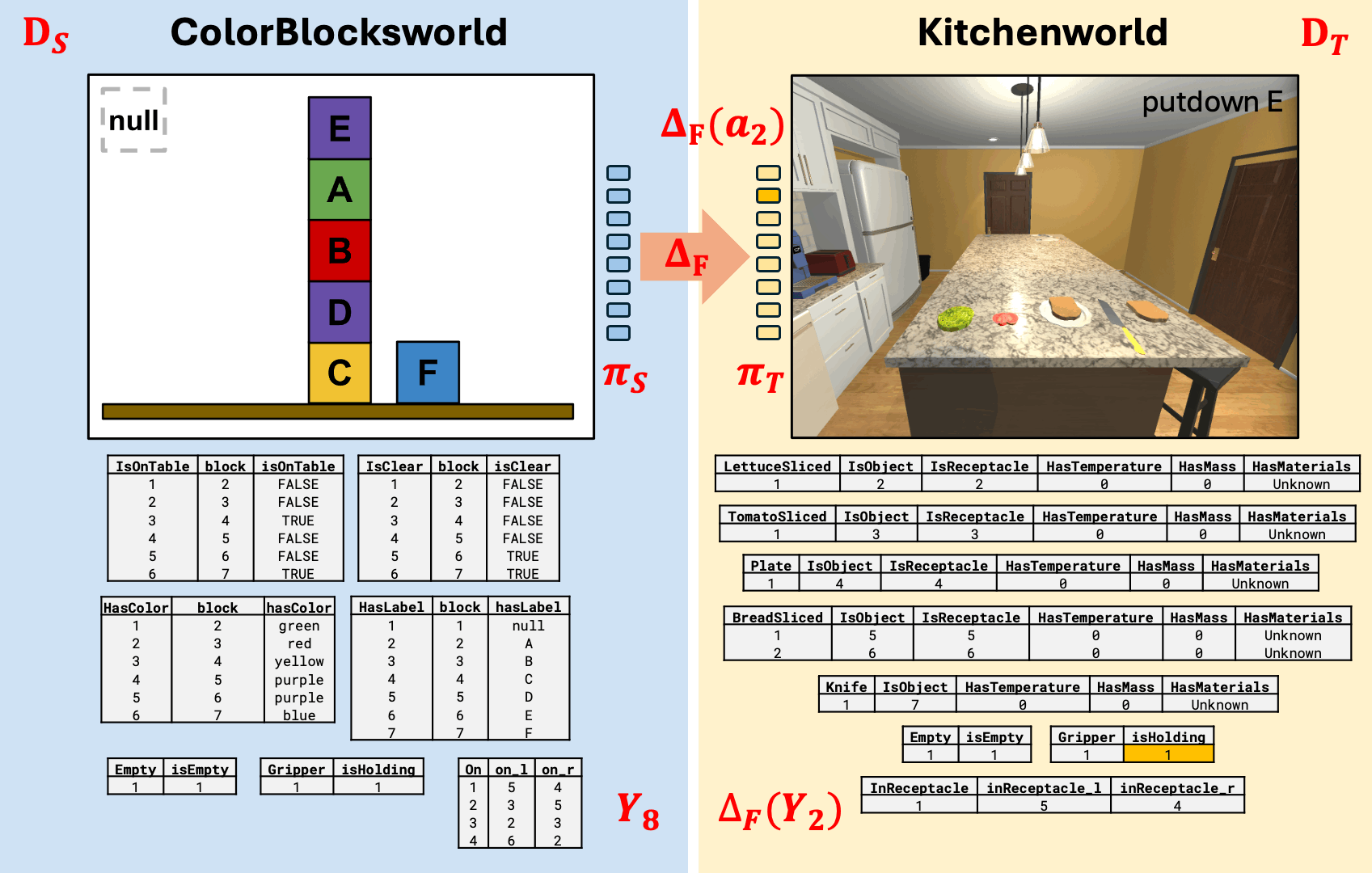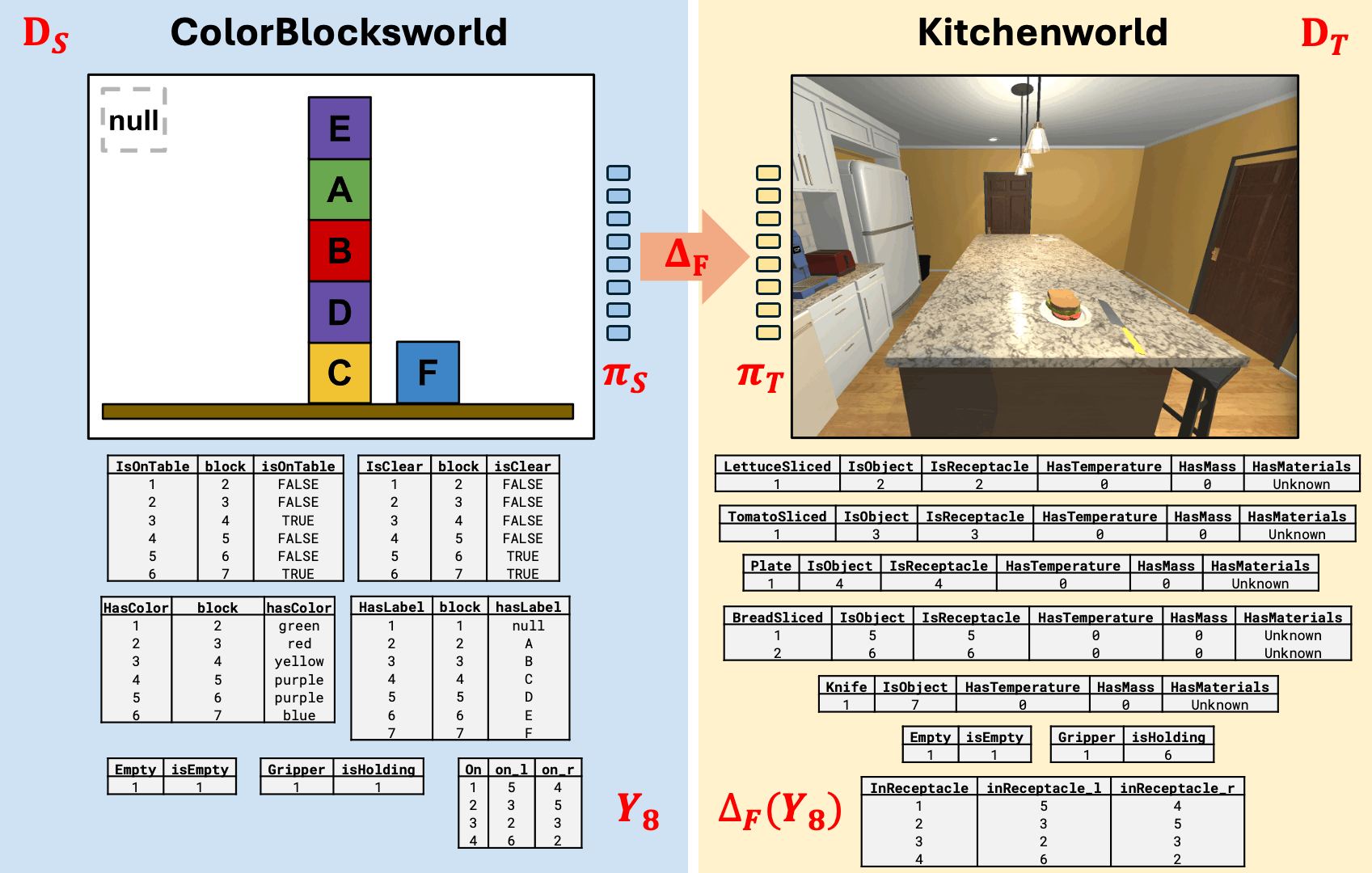
A \(\cat{C}\)-set, \(X\), that stores data about what boxes are on which surface.
The category of elements construction (Riehl 2016) makes \(X\) interoperable with RDF triple syntax (subject, predicate, object), facilitating its use in knowledge graphs (David I. Spivak and Kent 2012).
\(\cat{ColorBlocksworld}\)-set in Code
state = @acset_colim yColorBlocksworld begin
gripper::Gripper
empty::Empty
null::Block
isHolding(gripper) == null
isEmpty(empty) == null
(labelNull)::HasLabel
hasLabelDom(labelNull) == null
hasLabel(labelNull) == "null"
(A, B, C, D, E, F)::Block
(colorA, colorB, colorC, colorD, colorE, colorF)::HasColor
hasColorDom(colorA) == A
hasColorDom(colorB) == B
hasColorDom(colorC) == C
hasColorDom(colorD) == D
hasColorDom(colorE) == E
hasColorDom(colorF) == F
hasColor(colorA) == "green"
hasColor(colorB) == "red"
hasColor(colorC) == "yellow"
hasColor(colorD) == "purple"
hasColor(colorE) == "purple"
hasColor(colorF) == "blue"
(labelA, labelB, labelC, labelD, labelE, labelF)::HasLabel
hasLabelDom(labelA) == A
hasLabelDom(labelB) == B
hasLabelDom(labelC) == C
hasLabelDom(labelD) == D
hasLabelDom(labelE) == E
hasLabelDom(labelF) == F
hasLabel(labelA) == "A"
hasLabel(labelB) == "B"
hasLabel(labelC) == "C"
hasLabel(labelD) == "D"
hasLabel(labelE) == "E"
hasLabel(labelF) == "F"
(x1, x2)::On
onL(x1) == E
onR(x1) == D
onL(x2) == D
onR(x2) == C
(clearA, clearB, clearC, clearD, clearE, clearF)::IsClear
isClearDom(clearA) == A
isClearDom(clearB) == B
isClearDom(clearC) == C
isClearDom(clearD) == D
isClearDom(clearE) == E
isClearDom(clearF) == F
isClear(clearA) == true
isClear(clearB) == true
isClear(clearC) == false
isClear(clearD) == false
isClear(clearE) == true
isClear(clearF) == true
(onTableA, onTableB, onTableC, onTableD, onTableE, onTableF)::IsOnTable
isOnTableDom(onTableA) == A
isOnTableDom(onTableB) == B
isOnTableDom(onTableC) == C
isOnTableDom(onTableD) == D
isOnTableDom(onTableE) == E
isOnTableDom(onTableF) == F
isOnTable(onTableA) == true
isOnTable(onTableB) == true
isOnTable(onTableC) == true
isOnTable(onTableD) == false
isOnTable(onTableD) == false
isOnTable(onTableE) == false
isOnTable(onTableF) == true
end
pretty_tables(state)┌───────┬─────────┐
│ Empty │ isEmpty │
├───────┼─────────┤
│ 1 │ 1 │
└───────┴─────────┘
┌─────────┬───────────┐
│ Gripper │ isHolding │
├─────────┼───────────┤
│ 1 │ 1 │
└─────────┴───────────┘
┌──────────┬─────────────┬──────────┐
│ HasColor │ hasColorDom │ hasColor │
├──────────┼─────────────┼──────────┤
│ 1 │ 2 │ green │
│ 2 │ 3 │ red │
│ 3 │ 4 │ yellow │
│ 4 │ 5 │ purple │
│ 5 │ 6 │ purple │
│ 6 │ 7 │ blue │
└──────────┴─────────────┴──────────┘
┌─────────┬────────────┬─────────┐
│ IsClear │ isClearDom │ isClear │
├─────────┼────────────┼─────────┤
│ 1 │ 2 │ true │
│ 2 │ 3 │ true │
│ 3 │ 4 │ false │
│ 4 │ 5 │ false │
│ 5 │ 6 │ true │
│ 6 │ 7 │ true │
└─────────┴────────────┴─────────┘
┌───────────┬──────────────┬───────────┐
│ IsOnTable │ isOnTableDom │ isOnTable │
├───────────┼──────────────┼───────────┤
│ 1 │ 2 │ true │
│ 2 │ 3 │ true │
│ 3 │ 4 │ true │
│ 4 │ 5 │ false │
│ 5 │ 6 │ false │
│ 6 │ 7 │ true │
└───────────┴──────────────┴───────────┘
┌──────────┬─────────────┬──────────┐
│ HasLabel │ hasLabelDom │ hasLabel │
├──────────┼─────────────┼──────────┤
│ 1 │ 1 │ null │
│ 2 │ 2 │ A │
│ 3 │ 3 │ B │
│ 4 │ 4 │ C │
│ 5 │ 5 │ D │
│ 6 │ 6 │ E │
│ 7 │ 7 │ F │
└──────────┴─────────────┴──────────┘
┌────┬─────┬─────┐
│ On │ onL │ onR │
├────┼─────┼─────┤
│ 1 │ 6 │ 5 │
│ 2 │ 5 │ 4 │
└────┴─────┴─────┘Uses category theory programming framework provided by AlgebraicJulia
Planning Actions using Spans and DPO Rewriting
Definition: (\(\catSet{C}\)) The category \(\catSet{C}\) is a category whose objects are \(\cat{C}\)-set functors and whose morphisms are natural transformations.
A span in \(\catSet{C}\) is a diagram of shape (\(\bullet \leftarrow \bullet \rightarrow \bullet\)) in \(\catSet{C}\).
Actions are spans (\(\mathrm{Pre} \hookleftarrow \mathrm{Keep} \rightarrow \mathrm{Eff}\)) in \(\catSet{C}\)
Actions are applied to state \(X\) to produce state \(Y\) using Double-Pushout (DPO) Rewriting
(Aguinaldo et al. 2023), Section 6.4.2-6.4.4 in (Aguinaldo 2024)
\(\hookleftarrow\) is a monomorphism (e.g. injective function in \(\cat{Set}\)). \(\urcorner\) and \(\ulcorner\) is a pushout (e.g. quotiented disjoint union in \(\cat{Set}\)).
Actions in \(\catSet{ColorBlocksworld}\) in Code
unstack action span written in AlgebraicJulia
unstack = @migration SchRule OntColorBlocksworld begin
L => @join begin
gripper::Gripper
empty::Empty
(block, underblock, null)::Block
isEmpty(empty) == null
o::On
onL(o) == block
onR(o) == underblock
isHolding(gripper) == null
clearblock::IsClear
isClearDom(clearblock) == block
isClear(clearblock) == true
end
K => @join begin
(block, underblock, null)::Block
end
R => @join begin
gripper::Gripper
empty::Empty
(block, underblock, null)::Block
isEmpty(empty) == null
isHolding(gripper) == block
clearunderblock::IsClear
isClearDom(clearunderblock) == underblock
isClear(clearunderblock) == true
end
l => begin
null => null
block => block
underblock => underblock
end
r => begin
null => null
block => block
underblock => underblock
end
end;unstack action applied to the initial state \(X\)
Planning using \(\catSet{C}\) and DPO Rewriting
Existing state-space planning algorithms can be adapted to work with this planning representation (Section 6.4.4 in (Aguinaldo 2024)).
Example: ForwardPlan() executes depth-first search (DFS) to find a sequence of actions.
function ForwardPlan(world::ACSet, goal::ACSet, actions::Dict,
action_limits::Dict, action_usage::Dict,
plan::List)
# Exit criteria: goal is reached if there is a monic morphism from goal to world
if homomorphism(goal, world, monic=true) !== nothing
println("Goal reached.")
return plan
end
# Find applicable actions for the current world state
applicable = find_applicable_actions(world, actions)
# Backtrack criteria: no applicable actions
if length(applicable) <= 0
throw("No applicable actions found! Terminate path...")
end
# Iterate over all applicable actions
for action in applicable
action_name = action.first
match_morphism = action.second
# Backtrack criteria: action applied too many times
try
if action_usage[action_name] >= action_limits[action_name]
println("Abort path. Action used too many times.")
continue
end
catch
# Initialize action usage if it doesn't exist
action_usage[action_name] = 1
end
# Save current world state for backtracking
prev_world = world
selected_action = action[action_name].rule
# Apply the selected action to the current world state
try
world = rewrite(selected_action, world)
catch e
throw("Could not apply action!")
end
# Record the action and corresponding match morphism in the current plan
append!(plan, [selected_action => match_morphism])
try
# Recursively call ForwardPlan with updated world state
plan = ForwardPlan(world, goal, actions, action_limits,
action_usage, plan)
return plan
catch e
# Backtrack to previous world state if path fails
world = prev_world
pop!(plan)
println("Path failed. Try a different path.")
end
end
# If no valid plan is found, report failure
println("No plan found.")
endTransfer using Functorial Data Migration, \(\Delta_F\)
High-level Steps in Analogical Plan Transfer
- Define the Source Domain: Start by defining the ontology, \(\cat{D}_S\), and actions, \(A_S\), for the source domain, \(\textbf{D}_S\).
- Define the Planning Problem: Establish the initial and goal states, \(P_S = (I, G)\) within domain \(\textbf{D}_S\).
- Plan: Solve for a valid plan, \(\pi_S\), that solves for \(P_S\) within domain \(\textbf{D}_S\).
- Define the Target Domain Ontology: Specify the target ontology, \(\cat{D}_T\), in the new domain, \(\textbf{D}_T\).
- Align Ontologies: Create a translation map, \(F: \cat{D}_T \rightarrow \cat{D}_S\), linking the types and predicates from the target domain ontology to the source domain ontology.
- Transfer the Plan: Use the translation map to transfer the grounded plan via \(\Delta_F\), resulting in \(\pi_T\).
- Validate the Plan: Check that the end state after \(\pi_T\) contains \(\Delta_F(G)\).
Section 7.4 in (Aguinaldo 2024)
A review
Advantages and Limitations of Categorical Structure for Planning
Advantages
- Preserves ontological structure when applying actions and transferring plans
- Predictable runtime complexity w.r.t. PDDL and its extensions, e.g. typing and transitive closure constraints
- Generalized transfer for pair of domains
- Symbolic action (skill) generation
Limitations
- Reliance on advanced mathematical theory
- Higher runtime complexity for checking applicability of actions, \(O(n^k)\), w.r.t. PDDL, \(O(nk)\)
- Depends on proper (functorial) ontological alignment
- Difficulty handling structurally dissimilar domains
Section 6.6 and 7.8 in (Aguinaldo 2024)
Summary of Research Contributions
Purpose
Enable robots to reuse old task plans to solve new problems
Gap
In robot plan transfer, there is little attention given to task-level plan transfer.
Research Contributions
- Propose a conceptual framework for discussing types of task-level plan transfer, namely sequential, hierarchical, and analogical transfer
- Introduce a mathematical framework that validates each type of transfer based on symmetric monoidal categories, functors, \(\cat{C}\)-sets, DPO rewriting from category theory
- Use case studies to demonstrate effective applications of category theory to robotics and AI planning
Future Work
- Scaling studies and software tools for category theory-based planning and plan transfer
Areas of Future Work
Scaling Studies: Empirical and Theoretical
- More planning and plan transfer problems
- Scale by the size of the world state and ontology
- Scale by length of plan
- Design benchmarks, e.g. transfer accuracy
- Study functoriality of migration for certain ontology maps
A Software Tool for Category Theory-Based Planning and Transfer
- Run planners
- Automate discovery of functorial ontology alignments
- Perform analogical plan transfer
- Compose plans with other plans using sequential transfer
- Check plans satisfy abstract behavior using hierarchical transfer
Section 8.3 in (Aguinaldo 2024)
Knowrob (Tenorth and Beetz 2017) and Factory of the Future (Schäfer et al. 2021) ontologies
Research Highlights (1 of 2)
Papers and Pre-prints
- Aguinaldo, A., Patterson, E., Regli, W. Automating Transfer of Robot Task Plans using Functorial Data Migrations. arXiv pre-print (under revision IEEE-TASE 2024).
- Aguinaldo, A., Patterson, E., Fairbanks, J., Regli, W., & Ruiz, J. A Categorical Representation Language and Computational System for Knowledge-Based Planning. 2023 AAAI Fall Symposium on Unifying Representations for Robot Application Development - ⭐ Best Paper.
- Aguinaldo, A., Regli W. Modeling traceability, change information, and synthesis in autonomous system design using symmetric delta lenses. ICRA Compositional Robotics Workshop 2022.
- Aguinaldo, A., Regli W. Encoding Compositionality in Classical Planning Solutions. IJCAI Workshop on Generalization in Planning 2021.
- Aguinaldo, A., Regli W. A Graphical Model-Based Representation for Classical AI Plans using Category Theory. ICAPS 2021 Workshop on Explainable AI Planning.
- Aguinaldo, A., Bunker J., Pollard B., Shukla A., Canedo A., Quiros G., Regli W. RoboCat: A Category Theoretic Framework for Robotic Interoperability Using Goal-Oriented Programming. IEEE Transactions on Automation Science and Engineering, 2019. doi: 10.1109/TASE.2021.3094055.
Community Service
- ICAPS 2025 (International Conference on Automated Planning and Scheduling) Reviewer
- Co-author of Relational Thinking: From Abstractions to Applications (2024) digital textbook
- Open-source contributor to AlgebraicJulia
- Local organizer of the Applied Category Theory (ACT) conference, 2023
- Co-organizer of ICRA Compositional Robotics: Mathematics and Tools, 2023
- Co-organizer of The Adjoint School, 2022, 2023
- Student of The Adjoint School, 2021
Research Highlights (2 of 2)
Talks
- “Analogical Plan Transfer in Robotics using Functorial Data Migrations” at AMS Special Session on Applied Category Theory, II in 2025
- “‘What’s the plan?’, asked my robot” at JuliaCon in 2024
- “A Categorical Representation Language and Computational System for Knowledge-Based Planning” at AAAI Fall Symposium on Unifying Representations for Robot Application Development in 2023
- “A Category Theoretic Approach to Planning in a Complex World” at Microsoft Future Leaders in Robotics and AI Seminar Series in 2023
- “Contextual affordances in context-aware autonomous systems” at NIST Compositional Structures for Systems Engineering and Design Workshop in 2022 and AMS JMM 2023 Special Session on Applied Category Theory in 2023
- “Category theory for automated planning and program compilation in robotics” at Topos Berkeley Seminar in 2022
- “Applications of category theory to automated planning and program compilation in robotics” at Xerox PARC Design Seminar in 2022
- “Modeling traceability, change information, and synthesis in autonomous system design using symmetric delta lenses” at ICRA Compositional Robotics Workshop in 2022
- “Encoding Compositionality in Classical Planning Solutions” at IJCAI Workshop on Generalization in Planning in 2021
- “A Graphical Model-Based Representation for Classical AI Plans using Category Theory” at ICAPS Explainable AI Planning Workshop in 2021
- “Polynomial Functors in Catlab” at the Applied Category Theory Conference in 2021
- “Diary of a software engineering using categories” at Topos Institute: Berkeley Seminar and Lógicos em Quarentena (LQ) Seminar in 2021
- “Category Theory for Software Modeling and Design” at Hunter College Applied Mathematics Seminar in 2020
Acknowledgements
Research
- Bill Regli, UMD (Advisor)
- Dana Nau, UMD
- Yiannis Aloimonos, UMD
- Dinesh Manocha, UMD
- Huan Xu, UMD
- Mark Fuge, UMD/ETH Zurich
- Eswaran Subrahmanian, CMU/NIST
- Spencer Breiner, NIST
- Evan Patterson, AlgebraicJulia
- James Fairbanks, AlgebraicJulia
- Kristopher Brown, AlgebraicJulia
- Kevin Arlin, AlgebraicJulia
- Owen Lynch, AlgebraicJulia
- Brendan Fong, Topos Institute
- David Spivak, Topos Institute
- Jaime Ruiz, University of Florida
- Arquimedes Martinez Canedo, Siemens
- Jacob Bunker, ARLIS
- Gustavo Quiros Araya, Siemens
- Ankit Shukla, Siemens
- Lazlo Nemeth, Siemens
- Blake Pollard, former NIST
- Zinovy Diskin, McMaster Univ.
- Ian Levitt, NASA
- Andrew Cohen, Drexel University
Support
- Pedro Rodriguez, Johns Hopkins APL
- Michael Castle, Johns Hopkins APL
- Elisha Peterson, Johns Hopkins APL
- Emily Brown, Johns Hopkins APL
- Gina Marshall-Johnson, Johns Hopkins APL
- John Piorkowski, Johns Hopkins APL
- Matthew Dinmore, Johns Hopkins APL
- Rob Nichols, Johns Hopkins APL
- Bill Blackert, Johns Hopkins APL
- Christopher Gifford, Johns Hopkins APL
Funding
- Johns Hopkins University Applied Physics Lab Part-Time Study Program
- Adv. Robotics for Manu. ARM-18-01
- DARPA #HR00112220004
Friends and Family
- Priyaa Varshinee Srinivasan, Tallin Univ. of Tech.
- Joseph Moeller, Caltech
- Sophie Libkind, Topos Institute
- David Jaz Myers, Topos Institute
- Elena Di Lavore, Univ. of Pisa
- Nathan Haydon, Univ. of Waterloo
- Ana Luiza da Conceição Tenorio, U. São Paulo
- Daniel Cicala, Southern Connecticut State Univ.
- Nelson Niu, Univ. of Washington
- Paul Dancstep, “Relational Thinking”
- John Kanu, UMD
- Samuel Matos, Johns Hopkins APL
- Alison Albin, Johns Hopkins APL
- Gene Whipps, Johns Hopkins APL
- Vikram Saraph, Johns Hopkins APL
- Jonathan Cohen, Johns Hopkins APL
- Jose Aguinaldo
- Annie Aguinaldo
- Kristene Aguinaldo
- Alex Ly
Summary of Research Contributions
Purpose
Enable robots to reuse old task plans to solve new problems
Gap
In robot plan transfer, there is little attention given to task-level plan transfer.
Research Contributions
- Propose a conceptual framework for discussing types of task-level plan transfer, namely sequential, hierarchical, and analogical transfer
- Introduce a mathematical framework that validates each type of transfer based on symmetric monoidal categories, functors, \(\cat{C}\)-sets, DPO rewriting from category theory
- Use case studies to demonstrate effective applications of category theory to robotics and AI planning
Future Work
- Scaling studies and software tools for category theory-based planning and plan transfer
Appendix
Types of Analogies (in analogical plan transfer)
Data Migration for Each Type of Analogy
Direct Analogy using Delta Data Migration
Given a translation functor \(F: \cat{C}^{\prime} \rightarrow \cat{C}\), a delta migration functor, \(\Delta_F: \catSet{C} \rightarrow \catSet{C^{\prime}}\), is constructed as follows:
For a given object \(X\) in \(\catSet{C}\),
\(\Delta_F(X) = X \circ F\)
For a given morphism \(\alpha: X \rightarrow Y\) in \(\catSet{C}\), \(\Delta_F\) acts on \(\alpha\) to produce the following morphism in \(\catSet{C^{\prime}}\)—
\(\Delta_F(\alpha)_{c^{\prime}}: X(F(c^{\prime})) \rightarrow Y(F(c^{\prime}))\) for \(c^{\prime} \in \cat{C^{\prime}}\)
Direct Analogy
\(\Delta_F : \cat{C}^{\prime} \xrightarrow{F} \cat{C} \xrightarrow{X} \cat{Set}\)
Structural Analogy
\(\Delta_F : \cat{C}^{\prime} \xrightarrow{F} \cat{Diag^{op}(C)} \xrightarrow{F^\ast(X)} \cat{Set}\)
Structural Analogy using Conjunctive Query Data Migration
Given a translation functor \(F: \cat{C}^{\prime} \rightarrow \cat{Diag^{op}(C)}\) and a conjunctive query migration functor, \(\Delta_F: \catSet{C} \rightarrow \catSet{C^{\prime}}\), is constructed as follows:
For a given object \(X\) in \(\catSet{C}\),
\(\Delta_F(X) = F^\ast(X) \circ F\) where,
\(F^\ast(X): \cat{Diag^{op}(C)} \xrightarrow{\cat{Diag^{op}(X)}} \cat{\cat{Diag^{op}(Set)}} \xrightarrow{lim} \cat{Set}\)
Here, \((F^\ast(X))\) is the limit of the diagram \(F^\ast(X)\) computed in the category \(\cat{Set}\).
For a given morphism \(\alpha: X \rightarrow Y\) in \(\catSet{C}\), \(\Delta_F\) acts on \(\alpha\) to produce the following morphism in \(\catSet{C^{\prime}}\)—
\(\Delta_F(\alpha)_{c^{\prime}}: F^\ast(X)(c^{\prime}) \rightarrow F^\ast(Y)(c^{\prime})\) for \(c^{\prime} \in \cat{C}^{\prime}\)
Here, \((F^\ast(X))(c^{\prime})\) refers to the set obtained from \((F^\ast(X))\) at \(c^{\prime}\).
(David I. Spivak and Kent 2012), (Evan Patterson 2021), (David I. Spivak 2021)
String Diagram Viewer Demo
RoboCat Demo
Video Credit: Ankit Shukla (Siemens)
Why now?
| • | 2024 | Current applications in robotics span healthcare, search and rescue, education, food processing, etc. (Licardo, Domjan, and Orehovački 2024) |
| • • | 2023 | Survey of transfer learning in robotics (Jaquier et al. 2023), Categorical rewriting for \(\cat{C}\)-sets introduced (K. Brown et al. 2023) |
| • | 2021 | Programming with \(\cat{C}\)-sets implemented (Patterson, Lynch, and Fairbanks 2021) |
| • | 2015 | DARPA Robotics Challenge for disaster response applications (Defense Advanced Research Projects Agency (DARPA) 2015) |
| • • • | 2012 | Category theory for knowledge representation using functorial data migrations and \(\cat{C}\)-sets (David I. Spivak and Kent 2012), Deep Learning (Hinton et al. 2012) |
| • | 2009 | Survey of transfer learning for reinforcement learning domains (Taylor and Stone 2009) |
| • • | 2005 | Transfer learning for planning tasks (Fern, Yoon, and Givan 2006), DARPA Transfer Learning challenge (Gasser et al. 2005) |
| • | 1998 | PDDL - Planning Domain Definition Language introduced (Ghallab et al. 1998) |
| • | 1997 | Transfer learning between machine-learning tasks (Caruana 1997) |
| • | 1994 | Hierarchical Task Networks (HTNs) in planning introduced (Erol, Hendler, and Nau 1994) |
| • | 1991 | Graphical notation for monoidal categories (string diagrams) (Joyal and Street 1991) |
| • • | 1971 | STRIPS - Stanford Research Institute problem solver developed (Fikes and Nilsson 1971), Shakey robot - first robot using AI (Nilsson 1984) |
| • | 1954 | Unimate robot - first industrial robotic arm (Malone 2011) |
| • | 1945 | Category theory introduced (Eilenberg and MacLane 1945) |
AI
Robotics
Category Theory
Evolution of robot program reuse

Manual programming (F. Q. Brown 1967)
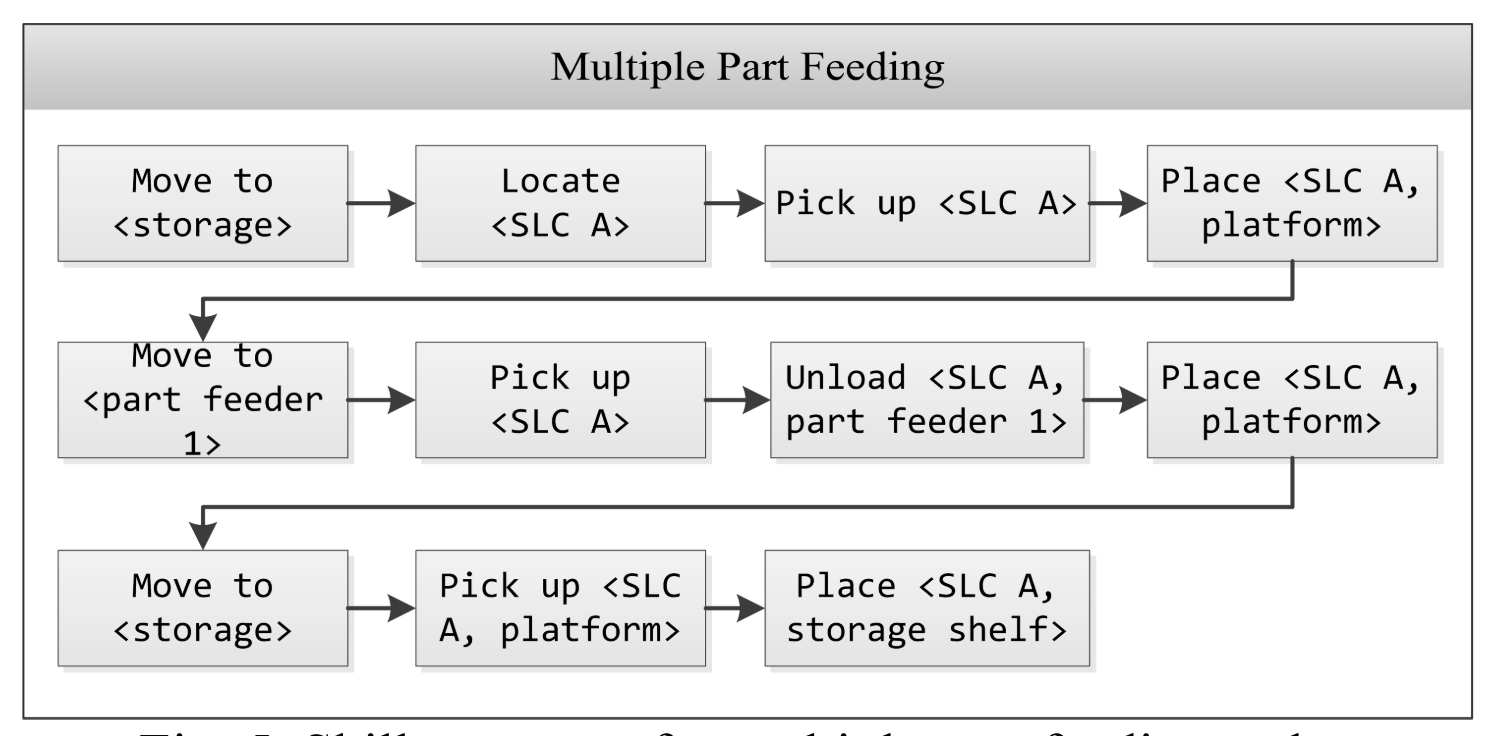

Motion primitives and skills
“Does your robot have skills?” (Bøgh et al. 2012), Assembly (Ionescu 2020), CRCL (Proctor et al. 2016)
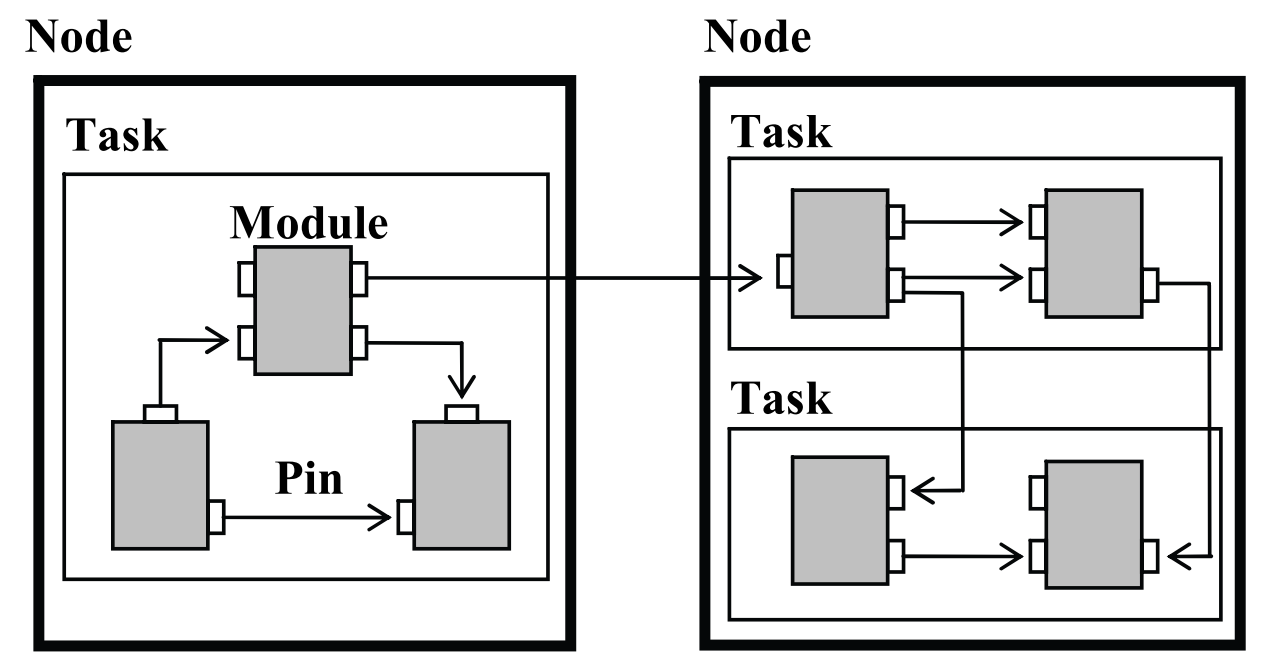
Modular architectures (Cowley, Chaimowicz, and Taylor 2006)



Middlewares (Aragão, Moreno, and Bernardino 2016), (Yang Liang 2008), (Matai et al. 2008)
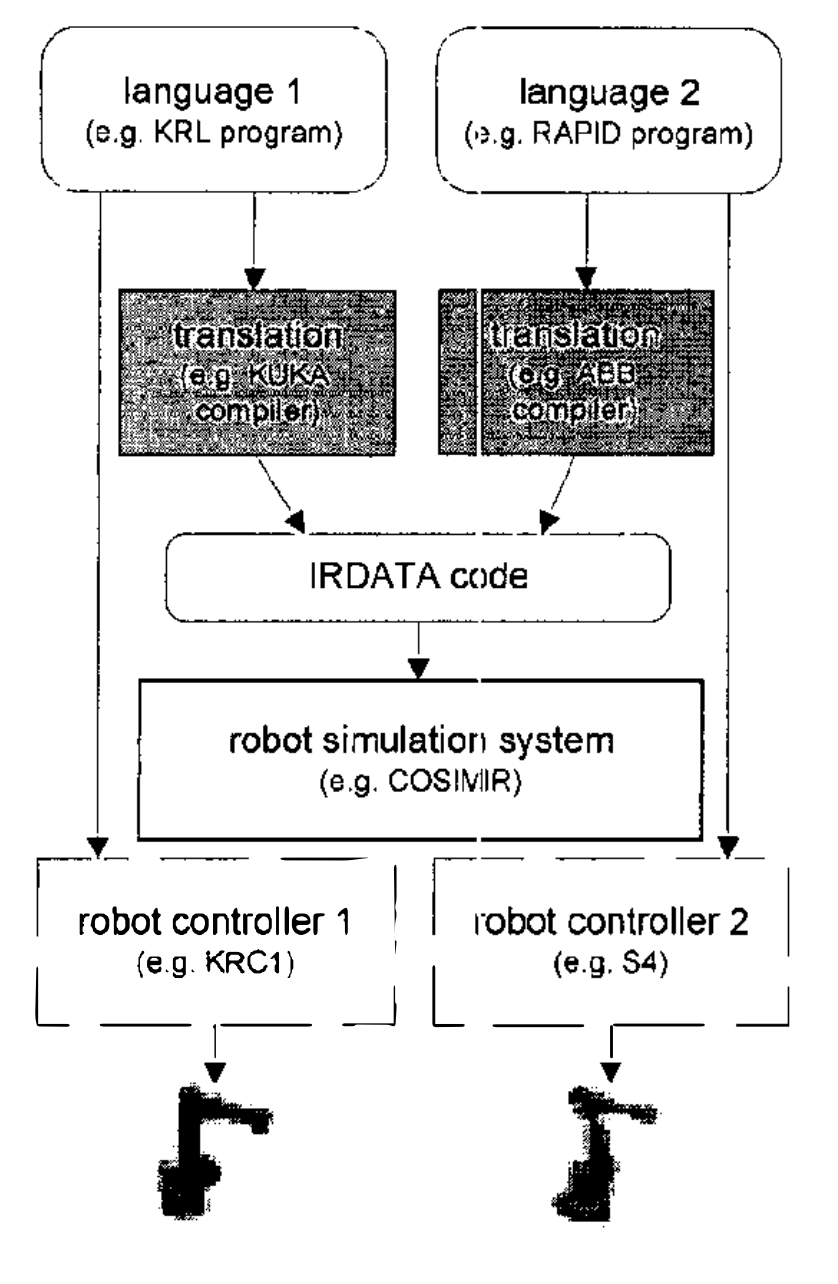
Program translation (Freund et al. 2001), (Freund and Luedemann-Ravit 2002)
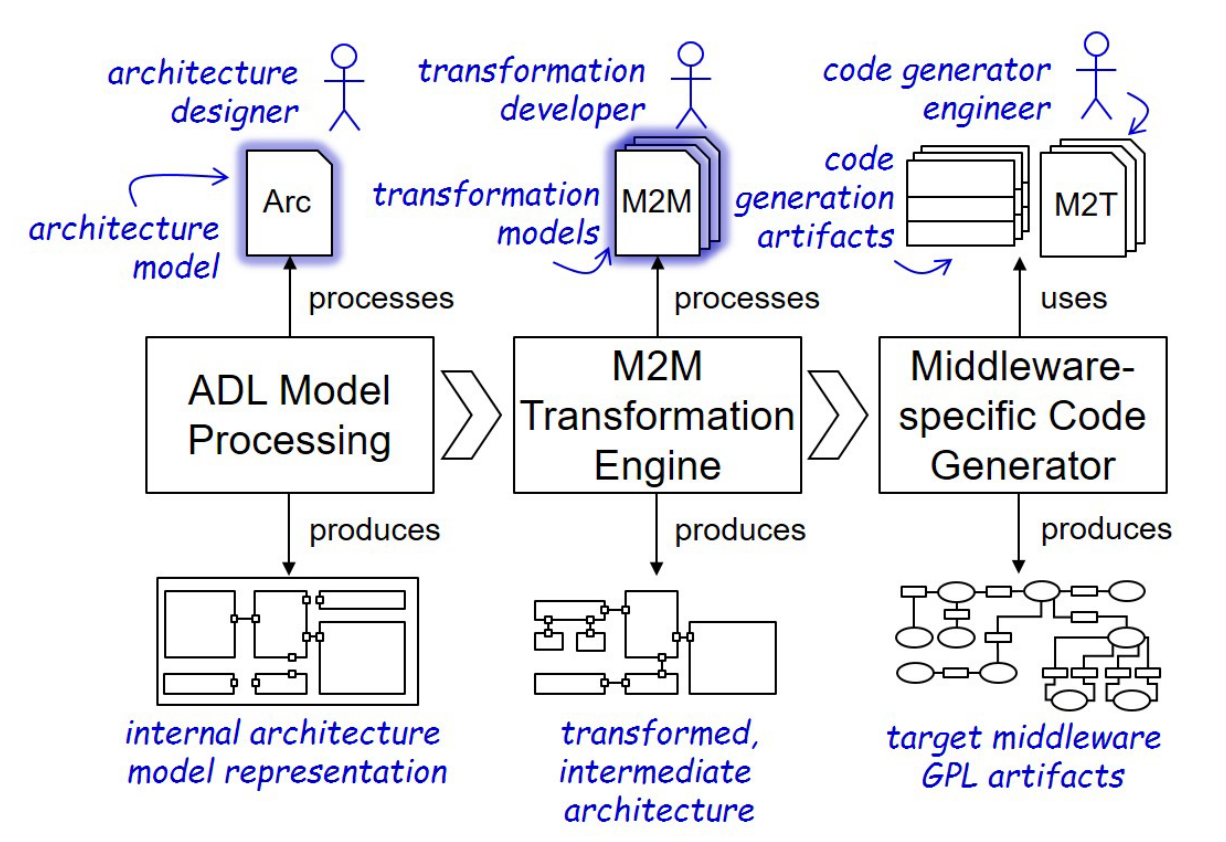
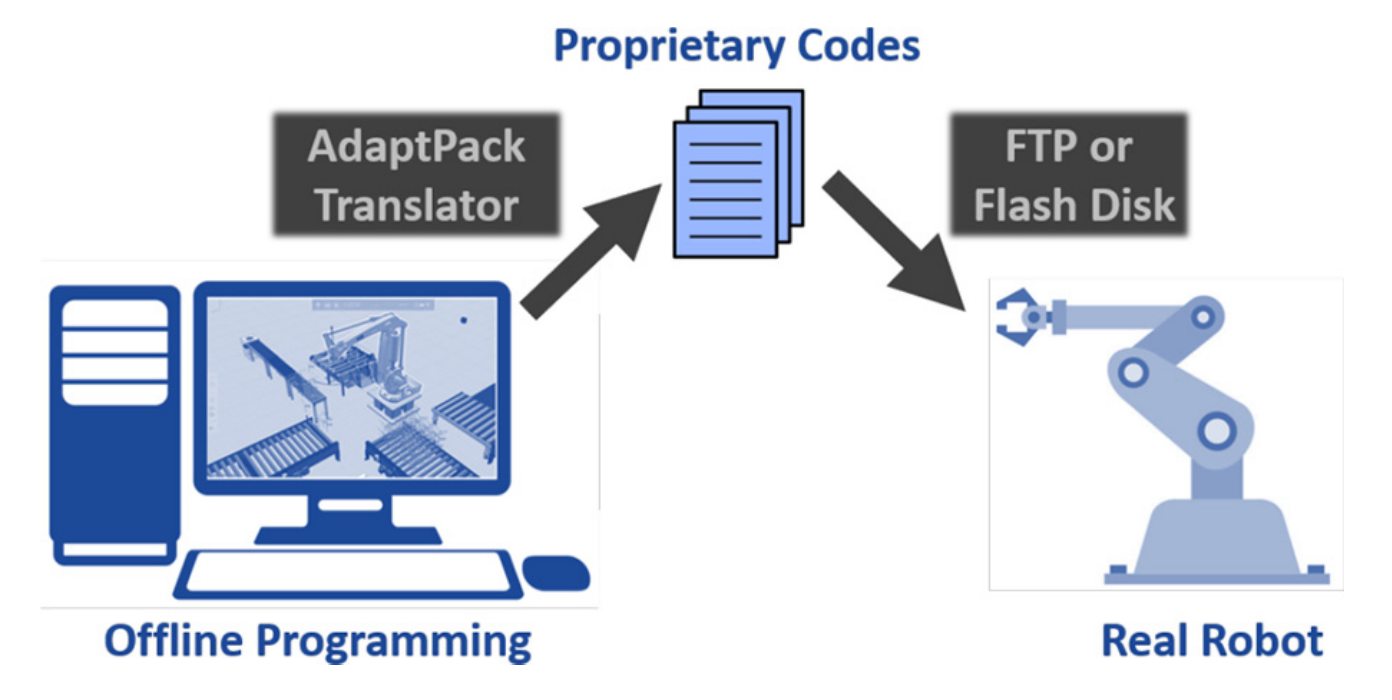
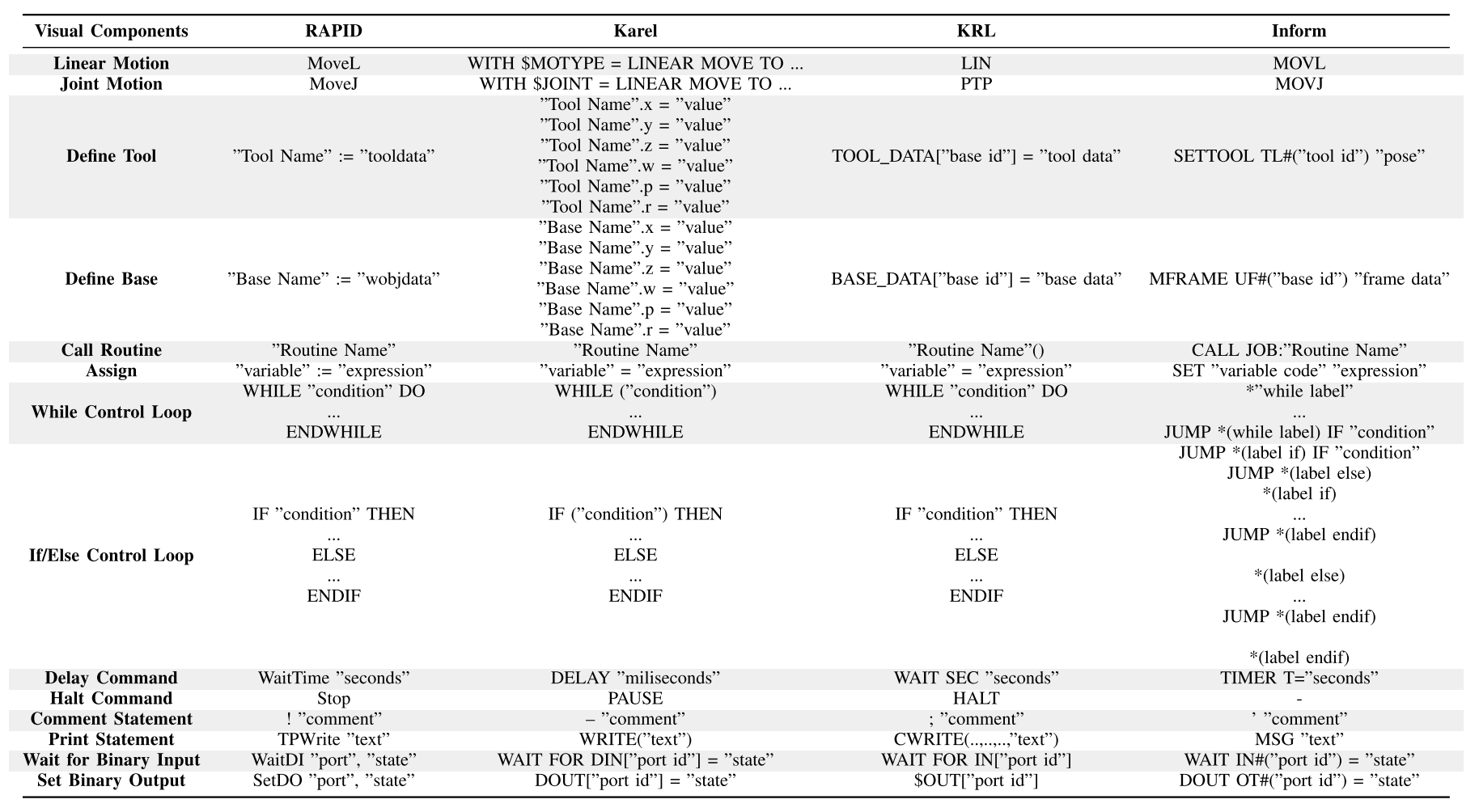
MontiArcAutomaton (Adam et al. 2017), (Ringert et al. 2014), AdaptPack Studio (Souza et al. 2019), (Carvalho de Souza et al. 2020)
References

Angeline Aguinaldo - Doctoral Defense - December 2, 2024

