using Catlab
using AlgebraicRewriting
@present OntBreadOnly(FreeSchema) begin
## Objects
Thing::Ob
BreadLoaf::Ob
BreadSlice::Ob
Countertop::Ob
Stool::Ob
## Morphisms
f::Hom(BreadSlice, BreadLoaf) # is part of
g::Hom(BreadLoaf, Thing) # is-a
h::Hom(Countertop, Thing) # is-a
l::Hom(Stool, Thing) # is-a
## Relations
InOn::Ob
inOn_l::Hom(InOn, Thing)
inOn_r::Hom(InOn, Thing)
end
# Create a C-set type based on ontology
const BreadOnly = DynamicACSet("BreadOnly", OntBreadOnly)A Categorical Representation Language and Computational System for Knowledge-Based Robotic Task Planning
AAAI Unifying Representations for Robot Application Development (URRAD) Fall Symposium 2023
October 25, 2023
Authors
 Angeline Aguinaldo
Angeline Aguinaldo
PhD Candidate
University of Maryland, College Park
Johns Hopkins University Applied Physics Laboratory
 Evan Patterson
Evan Patterson
Research Software Engineer
Topos Institute
 James Fairbanks
James Fairbanks
Assistant Professor
University of Florida
 William Regli
William Regli
Professor
University of Maryland, College Park
 Jaime Ruiz
Jaime Ruiz
Associate Professor
University of Florida
\[ \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\cat}[1]{\mathsf{#1}} \newcommand{\CAT}[1]{\mathsf{#1}} \newcommand{\Set}{\CAT{Set}} \DeclareMathOperator{\Path}{Path} \newcommand{\catSet}[1]{\cat{#1}\text{-}\Set} \DeclareMathOperator{\Ob}{Ob} \DeclareMathOperator{\Hom}{Hom} \]
1 Motivation & Related Work
1.1 Modeling real-world domains for task planning is hard
Let’s imagine ourselves as a domain modeler…
- Want to be able to model everything. Having many objects and relations in a scene can result in a combinatorial explosion of the search space due to the large number of facts.
- Want implicit ontological facts to be preserved after actions are applied. Implicit structure is not propagated when an action is applied, even when using domain axioms (Thiébaux, Hoffmann, and Nebel 2005).
- Want action models to be able to be defined generically. Because structure is not implicitly preserved, it is important that all action effects are accounted for in the action model.

1.2 How is it done today?
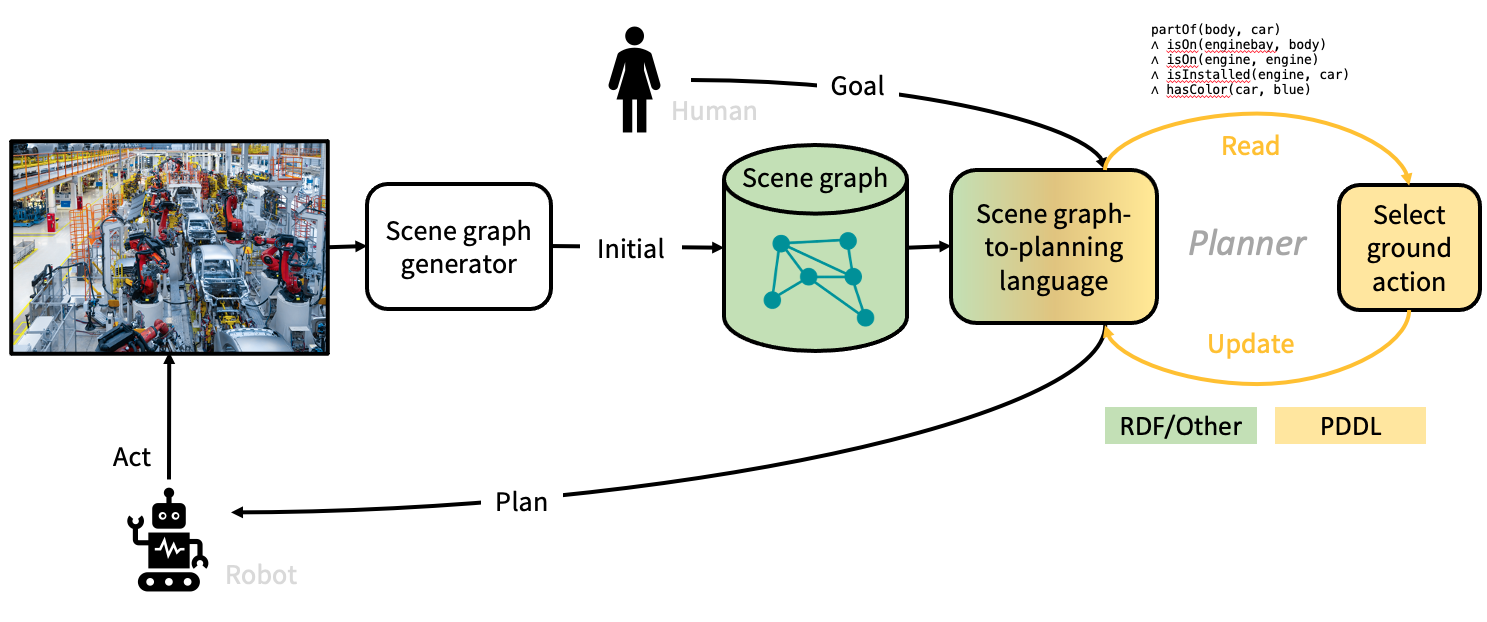 (Amiri, Chandan, and Zhang 2022),(Galindo et al. 2008),(Miao, Jia, and Sun 2023),(Agia et al. 2021)
(Amiri, Chandan, and Zhang 2022),(Galindo et al. 2008),(Miao, Jia, and Sun 2023),(Agia et al. 2021)
1.3 What is our proposed approach?
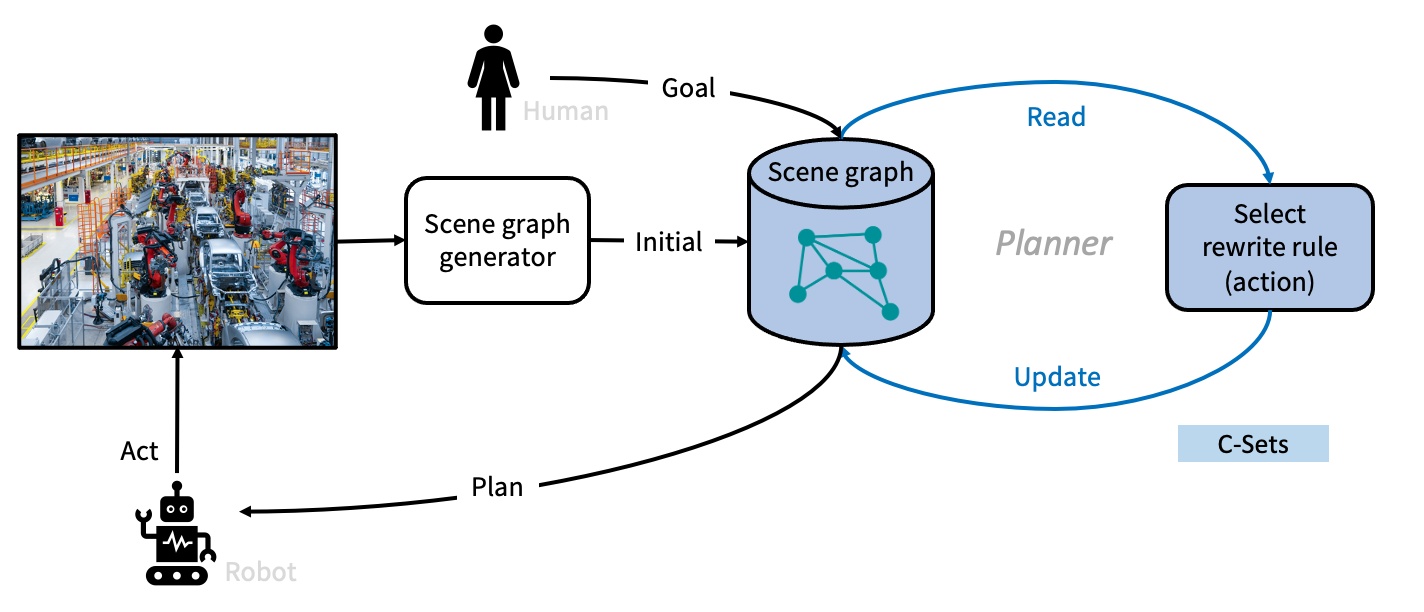
2 Category theory background
2.1 What is a category?
Definition: A category, \(\cat{C}\), consists of:
- a collection of objects, \(\text{Ob}(\cat{C})\)
- a collection of morphisms for every pairs of objects, \(\text{Hom}_\cat{C}(X,Y)\) for \(X, Y \in \text{Ob}(\cat{C})\)
- a composition operation, if \(f: X \rightarrow Y\), \(g: Y \rightarrow Z\) then \(g \circ f: X \rightarrow Z\)
- an identity morphism for every object, \(1_X: X \rightarrow X\)
satisfying the associativity law \(h \circ (g \circ f) = (h \circ g) \circ f\) and unitality laws \(f \circ 1_x = f\) and \(1_y \circ f = f\) whenever these equations make sense.
2.2 What is a functor and natural transformation?
Definition: A functor, \(F: \cat{C} \rightarrow \cat{D}\), from a category \(\cat{C}\) to a category \(\cat{D}\), has two components, \(F_0\) and \(F_1\), where:
\(F_0\) is a map between objects
\(F_0: \text{Ob}(\cat{C}) \rightarrow \text{Ob}(\cat{D})\)
\(F_1\) is a map between morphism sets
\(F_1: \text{Hom}_\cat{C}(X, Y) \rightarrow \text{Hom}_\cat{D}(F_0(X), F_0(Y))\)
such that,
- \(F_1(g \circ f) = F_1(g) \circ F_1(f)\) for \(f: X \rightarrow Y\) and \(g: Y \rightarrow Z\) in \(\cat{C}\)
- \(F_1(1_X) = 1_{F_0(X)}\) for every \(X \in \cat{C}\)
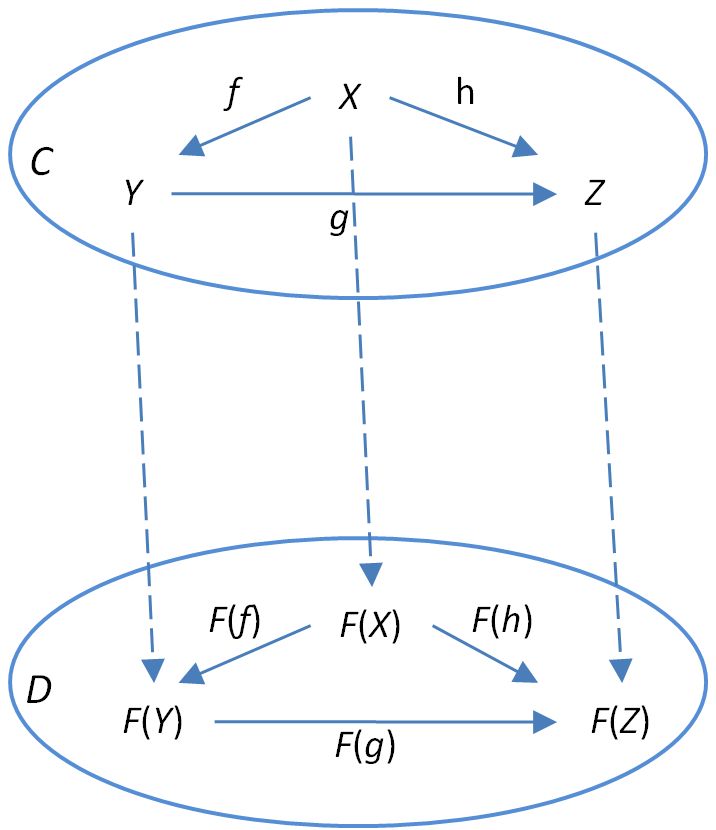 Taken from the nLab
Taken from the nLab
Definition: For functors, \(F: \cat{C} \rightarrow \cat{D}\) and \(G: \cat{C} \rightarrow \cat{D}\), a natural transformation between \(\alpha: F \rightarrow G\) that associates every object in \(C\) and with a morphism in \(D\) such that composition is preserved.
3 Approach: C-sets and Double-Pushout (DPO) rewriting
3.1 What is a C-set?
Definition: A \(\cat{C}\)-set is a functor from \(\cat{C} \rightarrow \cat{FinSet}\). \(\cat{FinSet}\) is a category whose objects are finite sets and whose morphisms are set function maps.
Example: An example \(\cat{C}\)-set, called \(G\), that stores data about people’s favorite pet.
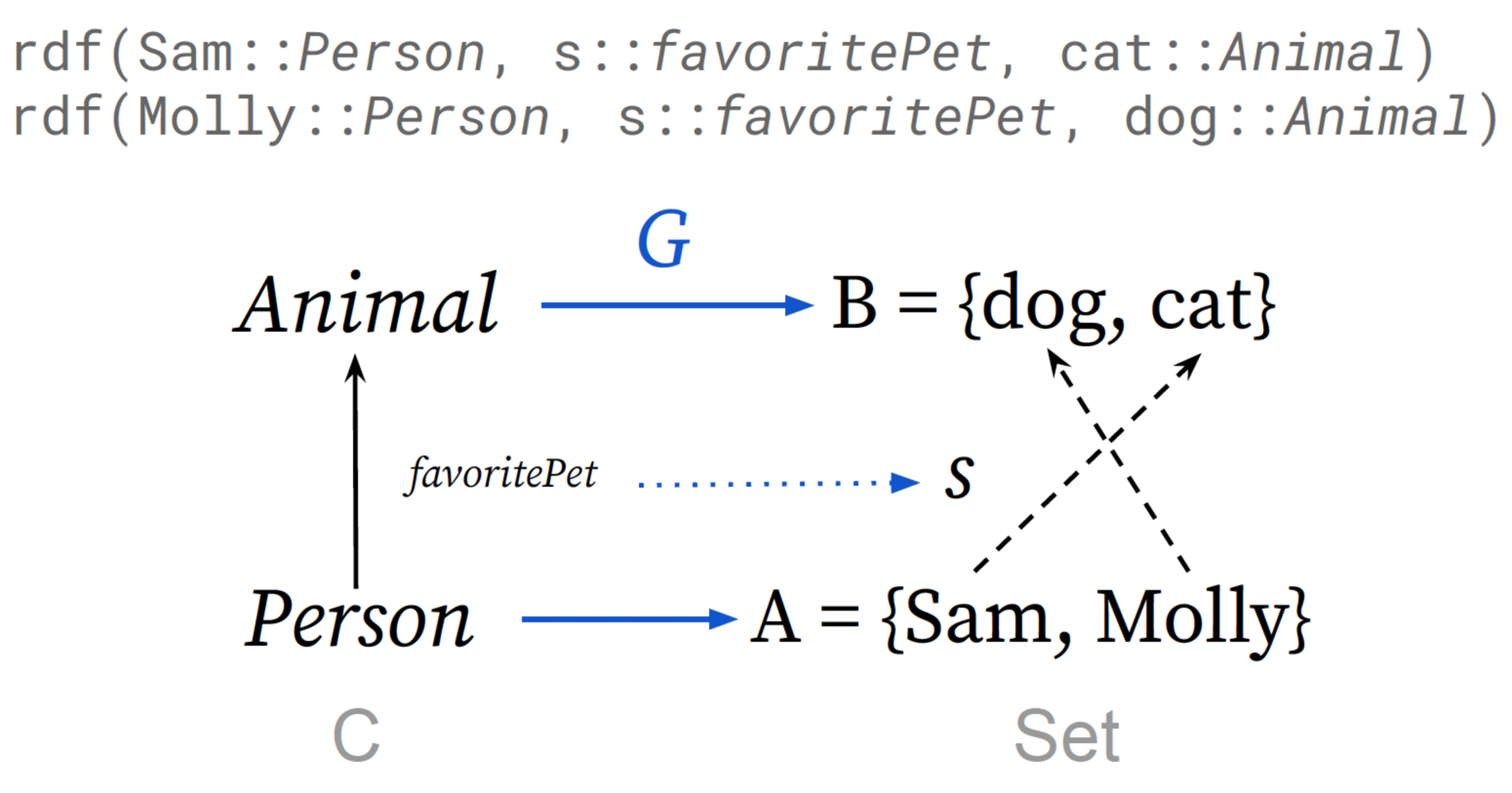
The category of elements construction (Riehl 2016) packages the data of \(G\) into a category resembling a knowledge graph (Patterson 2017).
3.2 What is Double-Pushout (DPO) rewrite rule?
Definition: The category \(\catSet{C}\) is a category whose objects are \(\cat{C}\)-set functors and whose morphisms are natural transformations.
Action rules are specified as spans in \(\catSet{C}\).
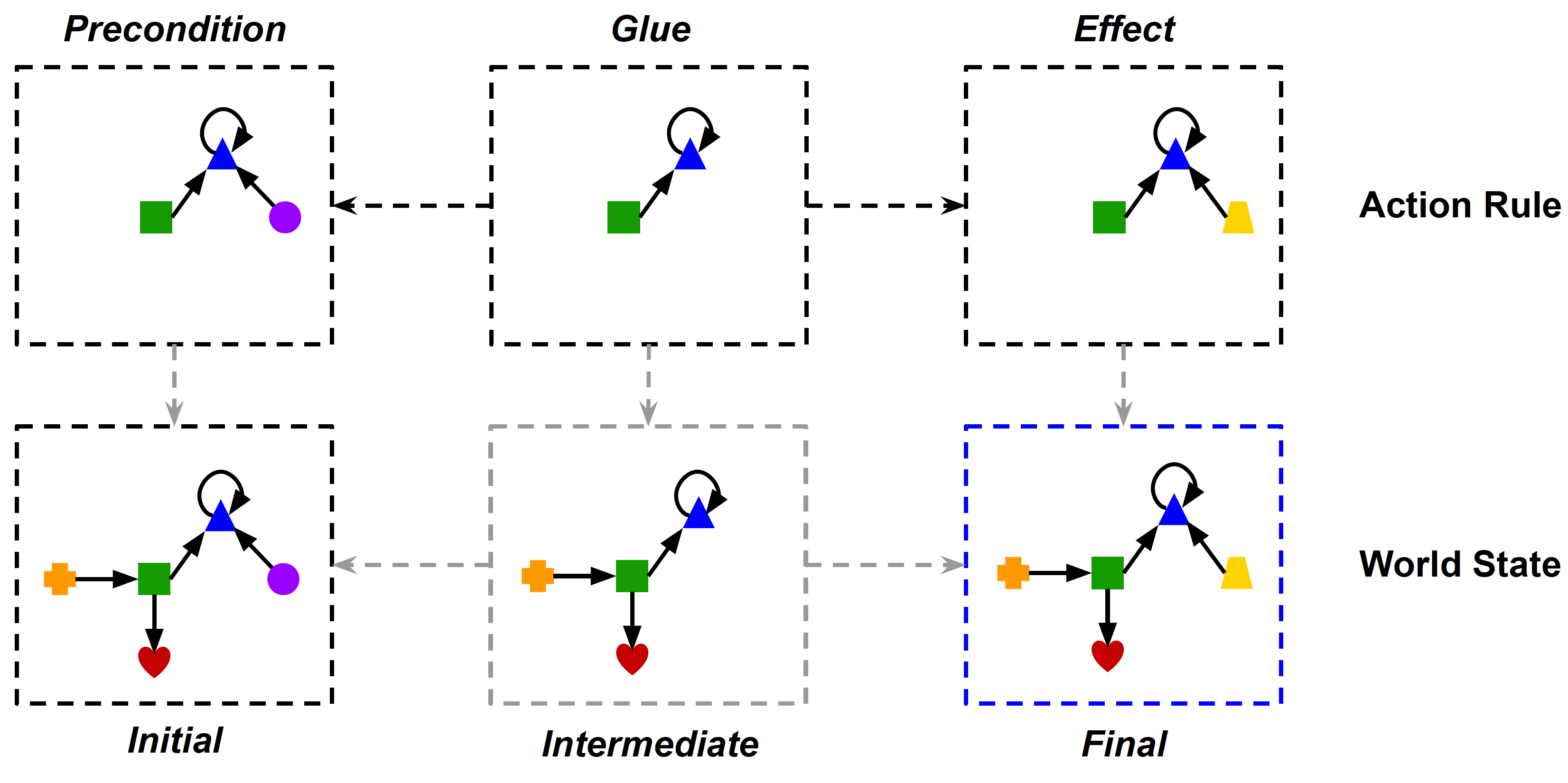
4 Let’s Plan!
4.1 Let’s define a world state
For more information about Catlab.jl and AlgebraicRewriting.jl, visit https://www.algebraicjulia.org/.

state = @acset_colim yBreadOnly begin
# Items in the scene
myCountertop::Countertop
myStool::Stool
naturesOwn::BreadLoaf
(slice0, slice1, slice2)::BreadSlice
# Nature's Own Breadloaf has three slices
# f::Hom(BreadSlice, BreadLoaf)
f(slice0) == naturesOwn # is part of
f(slice1) == naturesOwn # is part of
f(slice2) == naturesOwn # is part of
# Breadloaf is on countertop (relation)
thing_on_thing::InOn
inOn_l(thing_on_thing) == naturesOwn
inOn_r(thing_on_thing) == myCountertop
# Breadloaf, counterop, and stool are things
# g::Hom(BreadLoaf, Thing)
# h::Hom(Countertop, Thing)
# l::Hom(Stool, Thing)
(thing1, thing2, thing3)::Thing
g(naturesOwn) == thing1
h(myCountertop) == thing2
l(myStool) == thing3
end
pretty_tables(state)┌───────────┬───┐
│ BreadLoaf │ g │
├───────────┼───┤
│ 1 │ 2 │
└───────────┴───┘
┌────────────┬───┐
│ BreadSlice │ f │
├────────────┼───┤
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 1 │
└────────────┴───┘
┌────────────┬───┐
│ Countertop │ h │
├────────────┼───┤
│ 1 │ 1 │
└────────────┴───┘
┌───────┬───┐
│ Stool │ l │
├───────┼───┤
│ 1 │ 3 │
└───────┴───┘
┌──────┬────────┬────────┐
│ InOn │ inOn_l │ inOn_r │
├──────┼────────┼────────┤
│ 1 │ 2 │ 1 │
└──────┴────────┴────────┘4.2 Let’s define a rewrite rule
d = DRule(@migration(SchRule, OntBreadOnly, begin
L => @join begin
(thing1, thing2)::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
g(breadloaf) == thing1
h(countertop) == thing2
thing_on_thing::InOn
inOn_l(thing_on_thing) == breadloaf
inOn_r(thing_on_thing) == countertop
end
K => @join begin
thing::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
end
R => @join begin
(thing1, thing2)::Thing
breadloaf::BreadLoaf
countertop::Countertop
stool::Stool
g(breadloaf) == thing1
h(stool) == thing2
thing_on_thing::InOn
inOn_l(thing_on_thing) == breadloaf
inOn_r(thing_on_thing) == stool
end
l => begin
thing => thing1
breadloaf => breadloaf
countertop => countertop
stool => stool
end
r => begin
thing => thing1
breadloaf => breadloaf
countertop => countertop
stool => stool
end
end))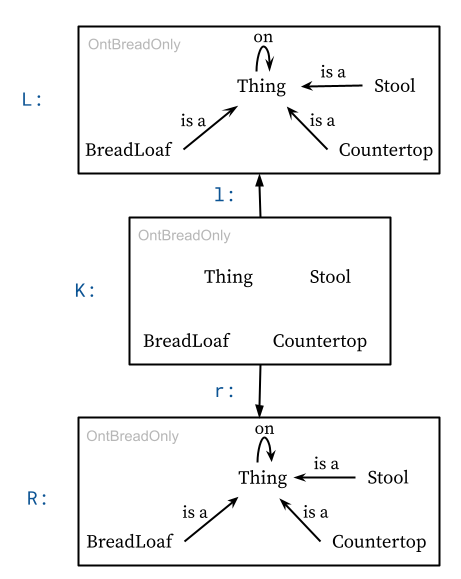
4.3 Let’s apply the rule
┌───────────┬───┐
│ BreadLoaf │ g │
├───────────┼───┤
│ 1 │ 1 │
└───────────┴───┘
┌────────────┬───┐
│ BreadSlice │ f │
├────────────┼───┤
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 1 │
└────────────┴───┘
┌────────────┬───┐
│ Countertop │ h │
├────────────┼───┤
│ 1 │ 3 │
└────────────┴───┘
┌───────┬───┐
│ Stool │ l │
├───────┼───┤
│ 1 │ 2 │
└───────┴───┘
┌──────┬────────┬────────┐
│ InOn │ inOn_l │ inOn_r │
├──────┼────────┼────────┤
│ 1 │ 1 │ 2 │
└──────┴────────┴────────┘
4.3.1 Ways rewriting can fail
- Dangling condition, unable to resolve mapping after the double pushout
- Objects are not properly identified because they not being included in the
K(keep) part of the rule
4.4 What does forward planning look like?
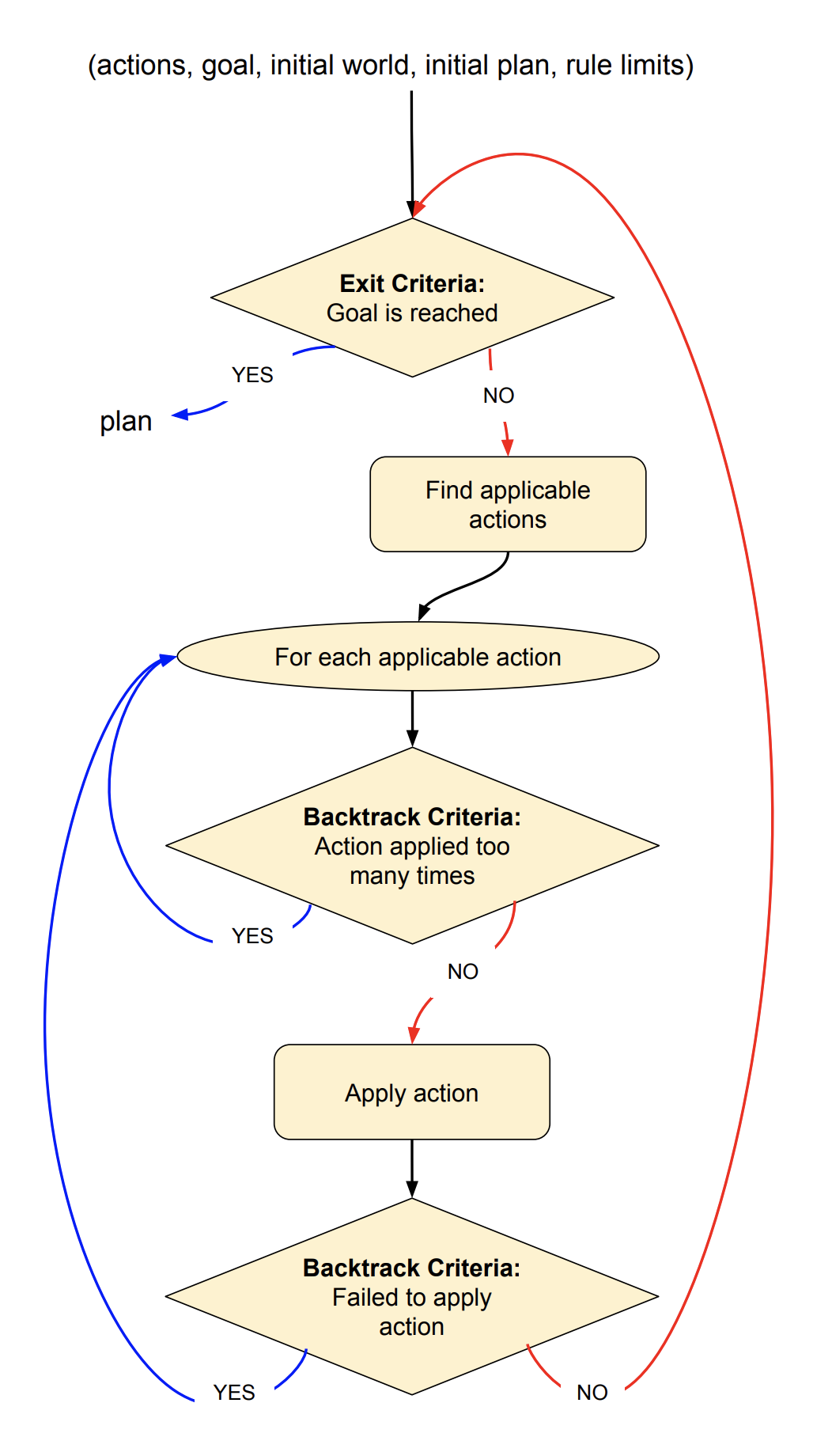
ForwardPlan(world::ACSet, goal::ACSet, rules_dict::Dict, rule_limits::Dict, config::FFConfig)
Executes forward planning search to find a sequence or all sequences of applicable DPO rewriting rules. A sequence of applicable DPO rewriting rules that transform an initial state to a goal state is called a plan.function ForwardPlan(world::ACSet, goal::ACSet, rules_dict::Dict, rule_limits::Dict, config::FFConfig)
# Exit criteria: goal is reached
if homomorphism(goal, world, monic=true) !== nothing
println("Goal reached.")
return plan
end
applicable = find_applicable_rules(world, rules_dict)
# Backtrack criteria: no applicable rules
if length(applicable) <= 0
throw("No applicable rules found! Terminate path...")
end
try
for rule_hom in applicable # try all applicable rules in order
selected = rule_hom.first
# Backtrack criteria: rule applied too many times
try
if config.rule_usage[selected] >= rule_limits[selected]
println("Abort path. Rule used too many times.")
continue
end
catch
config.rule_usage[selected] = 1 # fails if key doesn't exist, initialize
end
# apply rule and add to plan
prev_world = world
try
world = rewrite(rules_dict[selected].rule, world)
catch e
throw("Could not apply rule! " * string(e))
end
append!(config.plan, [rules_dict[selected].rule => rule_hom.second]) # include both rule and matched homomorphism
try
config.num_step =+ 1
config.plan = ForwardPlan(world, goal, rules_dict, rule_limits, config)
return config.plan
catch e
world = prev_world
pop!(config.plan)
println("Path failed. Try a different path.")
# println(string(e))
end
end
catch e
throw("Something went wrong with error: " * string(e))
end
println("No plan found.")
end5 Conclusion
5.1 Future Work
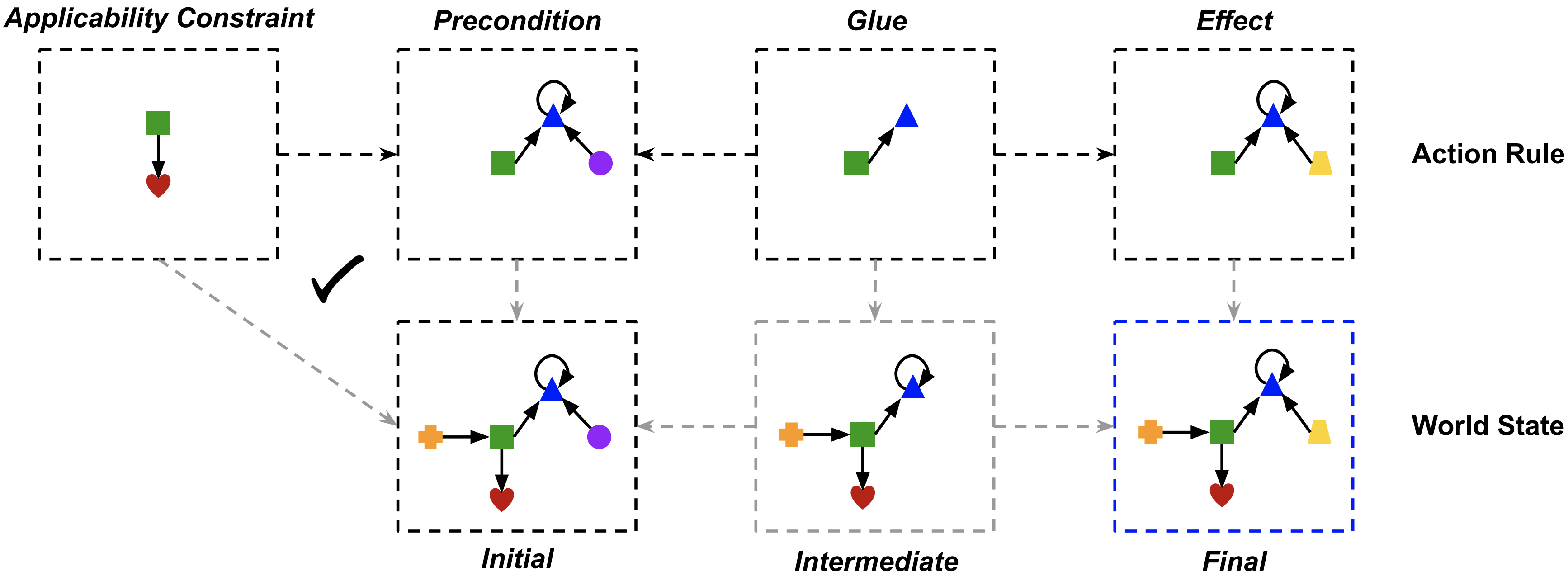
5.1.1 Parameterize action models using constraints
Leverage composition to factor out applicability constraints and parameterize generic action models
5.1.2 Migrating plans from one domain (ontology) to another
Use functorial data migration (Spivak 2012) to translate actions to new domain ontologies
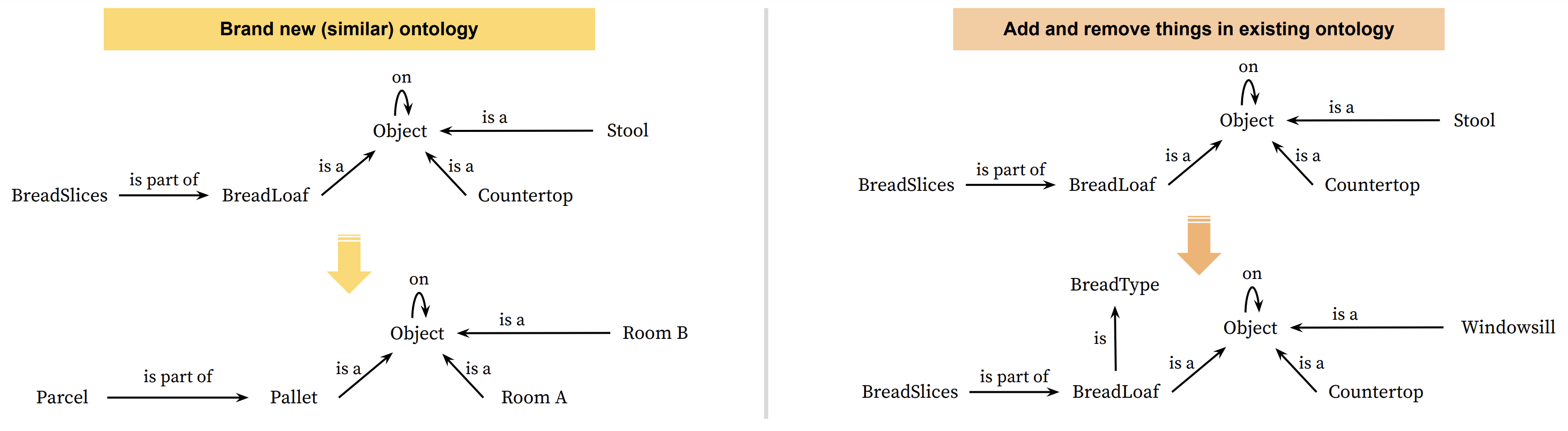
5.2 In Summary
- Our categorical representation allows a user to formalize the ontological model of the domain and instantiate structured knowledge based on the ontology.
- This method provides formal semantics for the use of knowledge graphs and relational databases to model world states and updates in planning.
- Future work include designing mechanisms for transferring plans between domains and extending this system to handle non-combinatorial data, such as numeric data.
5.3 Acknowledgements
- This work was partially funded by the U.S. Defense Advanced Research Projects Agency (DARPA) under contract #HR00112220004.
- We thank Kristopher Brown and Owen Lynch from the Topos Institute for heavily contributing to the development of DPO rewriting and \(\catSet{C}\) in AlgebraicJulia.
- We also thank the students of the Ruiz HCI Lab—Alexander Barquero, Rodrigo Calvo, Niriksha Regmi, Daniel Delgado, Andrew Tompkins—who built the task guidance platform that inspired the examples in this paper.
- We thank Dana Nau for valuable feedback about this paper.
5.4 References

AAAI Unifying Representations for Robot Application Development (URRAD) Fall Symposium 2023